For these questions it is better to get some counter examples by trying small graphs. Consider the following graph:
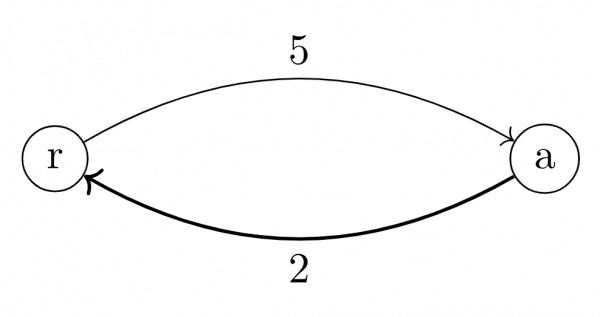
Now, as per the question, an arborescence is a subgraph with all incoming edges to the special vertex $r.$ So, for the above graph it is just the edge $a-r$ which is of weight $2.$
Now, option A says that if we sum up all the outgoing edge weights (minimum weight in case multiple outgoing edges exist) of all vertices excluding $r$, the sum will be greater than or equal to the weight of the minimum arborescence. This is true because all the edges in the minimum arborescence will be included here as the outgoing edges of the other vertices.
Now, option B is false. Because instead of outgoing edges we are adding the weights of incoming edges. And these edges are not part of the arborescence. For example, in the above graph, only one vertex $a \in V \backslash \{r\}.$
$ \sum_{u \in V \backslash \{r\}} \min_{(v,u) \in E} w((v,u)) = w(r,a) = 5 > w^*.$
Options C and D are straightforward TRUE as for minimum arborescence we only need to consider the incoming edges to $r$ from $n-1$ other vertices thus making it acyclic too.
For option E, suppose a graph has a directed Hamiltonian cycle. In an arborescence every vertex is connected and we need "one more" edge to make it a cycle. But this may or may not be a Hamiltonian cycle as a Hamiltonian cycle requires that in the path from the start and end of any vertex, no vertex is repeated. But if we take any directed Hamiltonian cycle, every vertex has a directed path to every other vertex (special vertex $r$ can be any of the given vertices) and so it is an arborescence. What will happen if we remove an edge $(u,v)$ from such a minimum weighted directed Hamiltonian cycle?. Then we no longer have a path to vertex $v$ but all vertices still have a path to vertex $u$ and so $u$ can be the special vertex making it still an arborescence. Since the weight of this edge $(u,v)$ is guaranteed to be positive, this means the weight of this arborescence must be STRICTLY less than the weight of the minimum Hamiltonian cycle. Thus option E is TRUE.
So, Correct answer: B.