We observe that given matrix A is a right stochastic matrix. That is, for every row the row sum is 1. What does that mean? It means the given matrix corresponds to some Markov system. which is: A 3 state system as follows : (with each edge being the probability of the system going from a state to other.)
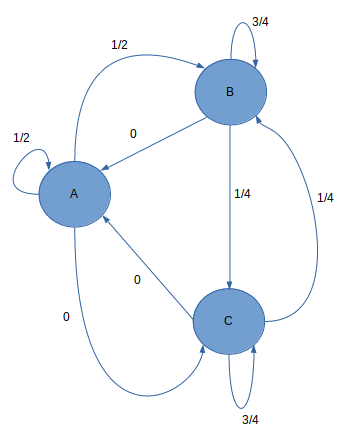
Now we find the steady-state probability vector as follows :
[$x_1 , x_2, x_3$] $\begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0 \\\\ 0 & \frac{3}{4} & \frac{1}{4} \\ \\ 0 & \frac{1}{4} & \frac{3}{4} \end{bmatrix}$ = [$x_1, x_2, x_3$]
As well as, we have $x_1 + x_2 + x_3 = 1$
Solving the above equation, we get $x_1 = 0, x_2 =\frac{1}{2}, x_3 = \frac{1}{2}$
We know that, in a Markov chain, $A^\infty$ is nothing but all rows steady-state vector.
Therefore, $A^\infty = \begin{bmatrix} 0 & \frac{1}{2} & \frac{1}{2} \\\\ 0 & \frac{1}{2} & \frac{1}{2} \\ \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix} $
Ref: If you want to know more about Markov chains and stochastic matrices: https://en.wikipedia.org/wiki/Stochastic_matrix#Definition_and_properties