In a Moore machine as we know each state has a fixed output. Hence suppose if we make a transition from one state whose output is 1 to another state, it will have a definite output defined for that state. In Mealy machine that is not the case the Automata accept an input symbol, generates an output symbol and if designed may or may not change states. Perhaps the diagram below will make it clear.
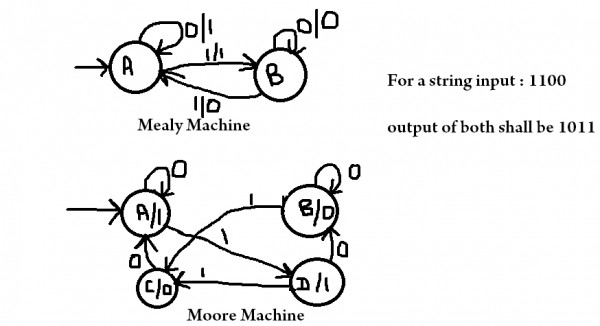
So for each state N in Mealy machine, we have Z number of states is Moore machine where Z=N*(number of output symbols). or Z=M*N
Z<N *(number of output symbol) or Z<N*M only when we define redundant states in Mealy Machine that is when further reduction is possible. Thus, a general answer $Z\leqslant M*N$