MadeEasy Full Length Test 2019: Combinatory - Generating Functions [closed]

Question

Let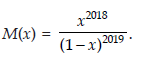 

 

We define Then ar is equal to.

 

• A. $\binom{r}{2019}$

• A. $\binom{r}{r + 2018}$

100. $\binom{r}{2019 – r}$

500. $\binom{r}{r – 2018}$

Can anyone tell me if this type of question is in Gate 2019 syllabus or not because I have never seen such question in previous year question? If yes, then when can I learn this stuff from.  Because I am unable to understand the whole solution.