GATE CSE 2019 | Question: 40

Question

Consider the following statements:

1. The smallest element in a max-heap is always at a leaf node
2. The second largest element in a max-heap is always a child of a root node
3. A max-heap can be constructed from a binary search tree in $\Theta(n)$ time
4. A binary search tree can be constructed from a max-heap in $\Theta(n)$ time

Which of the above statements are TRUE?

• A. I, II and III
• B. I, II and IV
• C. I, III and IV
• D. II, III and IV

Comments

When a heap is given, do we by default assume that it won’t contain any repeated values?

Because if the heap can contain repeated values (usually it doesn’t i guess) then 1 & 2 will be false and only 3 will be true.

---

@vin101 you are correct absolutely. But to all of you readers you should know that it proved that no comparison based sorting could be better than O(n*logn) so saying someone will find better is NULL and VOID. 

Reference : https://www.coursera.org/lecture/algorithms-divide-conquer/omega-n-log-n-lower-bound-for-comparison-based-sorting-advanced-optional-P2uwC

---

A max-heap can be constructed from a binary search tree in Θ(n) time

 

https://www.youtube.com/watch?v=MiyLo8adrWw&ab_channel=AlgorithmswithAttitude

 

Answer 1

1. The smallest element in a max-heap is always at a leaf node – TRUE because by definition of a max-heap every parent node must be larger than its child node.
2. The second largest element in a max-heap is always a child of a root node – TRUE. The $k^{\text{th}}$ largest element cannot have more than $k-1$ parents (larger value nodes) and so cannot be lower than level $k.$ 
3. A max-heap can be constructed from a binary search tree in $\Theta(n)$ time. Build heap for any array of size $n$ (even unsorted) can be done in $O(n)$ time.

Now lets see the $4^{\text{th}}$ statement. 

4. A binary search tree can be constructed from a max-heap in $\Theta(n)$ time. This can be proved $\textsf{FALSE}$ using the simple argument that we can do max-heap construction in $O(n)$ and if we can convert this to $\textsf{BST}$ in $O(n)$ time we can do an inorder traversal of $\textsf{BST}$ in $O(n)$ time and thus we manage to sort $n$ elements in $O(n)$ time using just comparisons which is known to take at least $\Omega(n \log n)$ time. 

---

An example construction of $\textsf{BST}$ from a max-heap. 

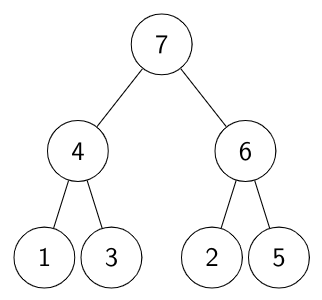
Max – Heap

Max Heap Array Representation: $$\begin{array}{|l|l|}\hline \text{Value}  &7&4&6&1&3&2&5  \\\hline \text{Array Index}  &  1&2&3&4&5&6&7  \\\hline \end{array}$$

Make binary search tree using Array Representation:

1. Pick elements from $A[1]$ to $A[7]$ one by one.
2. Compare with all previous elements and find its respective place.

We’ll get Binary Search Tree as follows:

Number of comparisons in the worst case for each element $=\underbrace{ \underset{\text{0}}{1} \quad \underset{\text{1}}{2} \quad \underset{\text{2}}{3} \quad \underset{\text{3}}{4} \quad \underset{\text{4}}{5} \quad \underset{\text{5}}{6} \quad \underset{\text{6}}{7}}^{\text{Elements}}_{\textbf{Comparisons}}$

So for $n$ element heap the total no of comparisons could be

$=0+1+2+\dots (n-2)+(n-1)$

$=\Theta \frac{(n-1)n}{2}$

$=\Theta (n^2)$

Note: Option IV: Proof by contradiction: Say you can somehow convert any arbitrary heap into a BST in $O(n)$ time.

It is already known that any arbitrary list can be converted into a heap in $O(n)$ time, and that the in-order traversal of BST is always sorted. So effectively we have sorted the array in linear time using comparison based sorting technique, but that is not possible as any comparison based sorting requires $\Omega(n \log n)$ time. That is a contradiction.

By using more efficient method this time complexity could be reduced to $O( n.\log n)$ but it can never be $ O(n)$.

OPTION A is the correct answer.

Comments

how this can be done in 0(nlogn) time.when we delete every time the max.element from heap we will get a sorted desc.order,now when we will construct bst out of it how much time will it take n or n^2

---

Heap is nothing but an array , so traverse array elements in a loop and follow normal insertion algo. of BST, to insert n elements of array, it takes “nlogn” time in worst case.

---

As insertion of n elements take O(n) time and BST best case is if it is height balanced and worst if it is skewed..so O(nlogn) or O(n^2) respectively

---

For nlogn we can do:

1. Apply heap sort on the heap. Now we have a sorted list of numbers. O(nlogn)
2. Convert the sorted list of numbers into a balanced BST. O(n)

Total = O(nlogn) + O(n) = O(nlogn)

Answer 2

$1$ and $2$ can be shown by simply taking examples

and $3$ is build heap time complexity

so $1,2$ and $3$ are true.Answer is (A).

Comments

@Dharmendra TiwariCan you explain option $4$ in great detail? Why it is false and how much time it will take?

---

Statement (IV) is false, because construction of max-heap from binary search tree will take O(nlogn) time

 

---

@Nitesh Singh 2

See the comment below the question.

The best comment.

Some people had doubt regarding 4th option. A good contradictory statement that would have helped fellow exam takers rule out this option is that if we could have created bst out of heap in O(n) time then we have got a method to get sorted order of keys in linear time(using an inorder traversal) which we know is not possible as the lower bound on comparison based sorts is O(nlogn) or else if we had other ideas Turing award was there for the taking.

Answer 3

The smallest element in a max-heap is always at a leaf node because of the max heap property.

Statement I is correct.

---

The nth largest element in a max heap is always present in the first n levels of the heap.

So, the second largest element can be at Level 1 or Level 2.

Can't be at Level 1 because that position is secured for the maximum value.

So, Level 2. Hence, child of the root.

Statement II is correct.

https://stackoverflow.com/questions/50940998/finding-the-7th-smallest-element-in-min-heap

---

Converting BST to min or max heap takes $\Theta (n)$ time. Just call build heap.

(Heapify will not work, as the binary search tree could be skewed and therefore node-to-index distribution in the array may not have a pattern, and we might need to traverse the entire array)

Statement III is correct.

---

To convert heap to BST, we need to find the correct place of each node.

At each level, what we do is compare, then put the element to it's correct place.

This is just like comparison based sorting, for which we know that the lower bound is nlogn.

So, can't be $\Theta(n)$

Statement IV is incorrect.

---

Option A

Answer 4

Ans: A

 

I. It is trivial. The smallest element is present in any one of the leaf nodes. TRUE

II. This is also always true to satisfy max heap property. Assume here distinct heap elements. TRUE

III. To access the elements in a BST we can do a traversal which will take O(n). Now to insert into max heap we need O(lg n) per insertion so time complexity O(n lg n) but a more strict bound is O(n) because for every insertion we don't need O(lg n) time but instead some constant time O(1). So O(n) + O(n) = O(n). TRUE

IV. For extraction from max heap we need O(lg n) but for inserting into a BST the total time taken would be O($n^2$) since it will get skewed and insertion time would be like O(1+2+3+4.. n) = O($n^2$). FALSE 

Comments

@Tuhin Dutta

U can write in order traversal in O(n) time and store these numbers in an array,u will get some sorted order and in these numbers, u can apply build heap procedure which takes O(n) time...So overall time will be O(n) time only...

---

@akash.dinkar12 what about cost of sorting?

---

@manisha11 Build-Heap() doesn't need sorted array as input.