Statement 1 is Correct but Statement 2 is Incorrect.
Statement 1 : If $f$ and $f _o g$ are one to one, then it follows that $g$ is one to one.
Moreover, We don't even need $f$ to be One One. i.e. We have the following result :
If $f_og$ is One One then $g$ is One One.
Proof :
We can use proof by Contradiction here.
So, Given that $f$ and $f_og$ are One to One. Let's assume that $g$ is Not One to one.
Since $f_og$ is One One, so, $(f_og(a) = f_og(b)) \rightarrow (a= b)$
Since $g$ is Not one to one, so, $\exists x,y (x\neq y \wedge (g(x) = g(y)))$
Since $g(x) = g(y)$, so, $f(g(x)) = f(g(y))$ i.e. $f_og(x) = f_og(y)$ which should mean that $x = y$ (because $f_og$ is One One) But we know that $x \neq y.$ Which is a Contradiction.
So, If $f_og$ is One One then $g$ is One One.
Statement 2 : if $f$ and $f _o g$ are onto, it follows that $g$ is onto.
This statement is Wrong. We can give a Counter example for this statement :
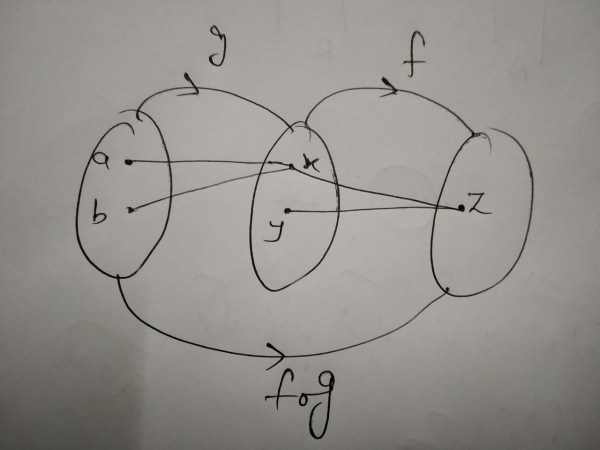
Clearly, $f$ and $f_og$ are Onto But $g$ is Not Onto.