${\color{Red}{Literals:} }$Every occurrence of the variables in it's true(pure) and complemented(negation) forms.
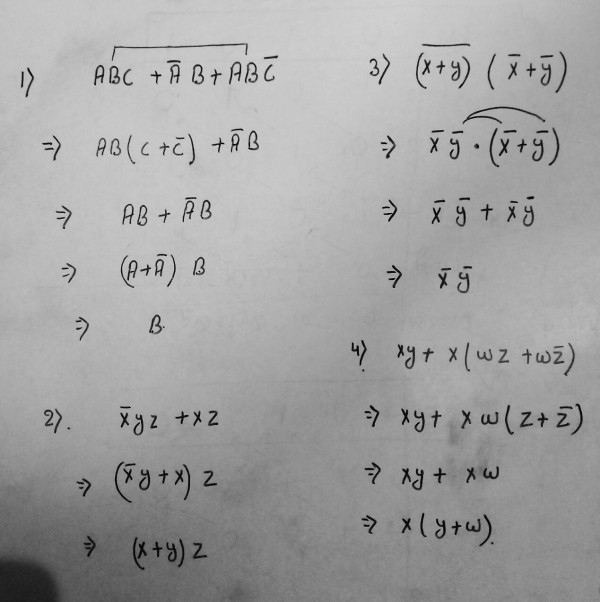
$(5)$$(BC’ + A’D)(AB’ + CD’)$ Here number of literals$ = 8$
we can write like this
$\Rightarrow BC'AB'+BC'CD'+A'DAB'+A'DCD'$
$\Rightarrow ABB'C'D+BC'CD'+A'AB'D+A'CDD'$
$\Rightarrow 0+0+0+0=0$ $\left [ X.X'=0\right ]$ Here number of literals $ = 0$