Fatima traverses like this:-
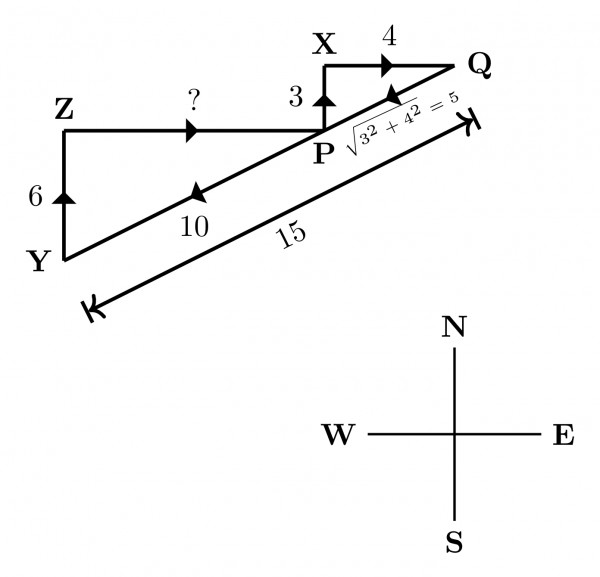
Making right angle triangles, $\unicode{0x25FA} \: PXQ$ & then $ \unicode{0x25FA} \: PZY$.
So, to reach point $P$ from $Y$ she has to travel =$\sqrt{(10^2-6^2)} = 8 \: km$. (in East direction)
Hence, Correct Answer: $ A. \: 8 \: km, \: East $