We know that $2^n$ would always be greater than $2*n$(exponential increase > linear increase) after a certain point.
We just need to find that point.
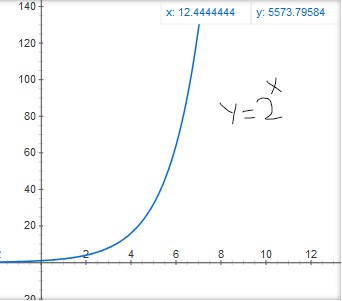
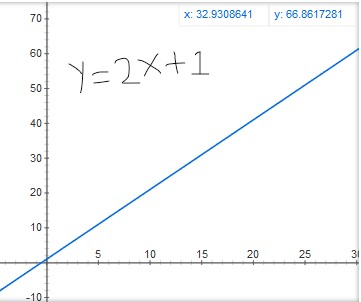
The intersection point would occur when
$2^n = 2n+1$
On solving this we get $n \approx 2.6$.
Now after this i.e. after $n=2.6$ the inequality would hold for all values of $n$
$\therefore$ Option $A.$ is correct answer.