ISI2015-DCG-12

Question

The highest power of $3$ contained in $1000!$ is

• A. $198$
• B. $891$
• C. $498$
• D. $292$

Answer 1

$1000! = 1000*999*998*997.....1$

$3,9,27,81,243,729$ are the powers of $3$ present in $1000!$

 

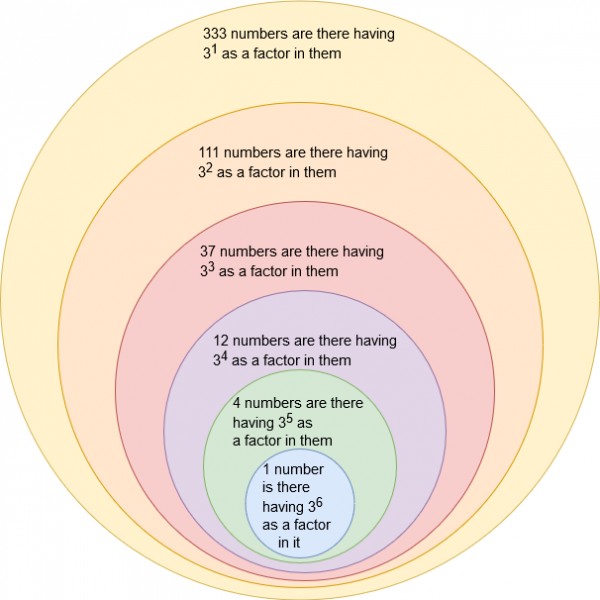
$729$ has no multiple present in $1000!$ except itself i.e. $3^6$

so we can say we have $1$ number only in which $3^6$ is coming

 

$243$ has $4$ multiples present in $1000!$ i.e. $243,486,729,972$ = $(3^5*1),(3^5*2),(3^5*3),(3^5*4)$

so we can say we have $4$ numbers in which $3^5$ is coming.

 

$81$ has $\frac{1000}{81}=12$ multiples present in $1000!$ i.e. $(3^4*1),(3^4*2),.....,(3^4*12)$

so we can say we have $12$ numbers in which $3^4$ is coming.

 

$27$ has $\frac{1000}{27}=37$ multiples present in $1000!$ i.e. $(3^3*1),(3^3*2),.....,(3^3*37)$

so we can say we have $37$ numbers in which $3^3$ is coming.

 

$9$ has $\frac{1000}{9}=111$ multiples present in $1000!$ i.e. $(3^2*1),(3^2*2),.....,(3^2*111)$

so we can say we have $111$ numbers in which $3^2$ is coming.

 

$3$ has $\frac{1000}{3}=333$ multiples present in $1000!$ i.e. $(3*1),(3*2),.....,(3*111)$

so we can say we have $333$ numbers in which $3$ is coming.

 

 

Hence the highest power of $3$ in $1000! = 333+111+37+12+4+1 = 498 $

$\therefore$ Option $C.$ is correct.

 

Comments

$\left \lfloor \dfrac{1000}{3}\right \rfloor = 333$

$\left \lfloor \dfrac{333}{3}\right \rfloor = 111$

$\left \lfloor \dfrac{111}{3}\right \rfloor = 37$

$\left \lfloor \dfrac{37}{3}\right \rfloor = 12$

$\left \lfloor \dfrac{12}{3}\right \rfloor = 4$

$\left \lfloor \dfrac{4}{3}\right \rfloor = 1$

$\left \lfloor \dfrac{1}{3}\right \rfloor = 0$

The highest power of $3$ contained in $1000!$ is $ = 333+111+37+12+4+1+0 = 498$