Answer: $\mathbf B$
Explanation:
Algebraic solution:
$\Big({\underbrace{\frac{9}{10}}}_{\bf{+ve}}\Big)^x = -(x^2-x+3) = -\Big(x^2-2.\frac{1}{2}x+(\frac{1}{2})^2+3(\frac{1}{2})^2\Big) =\underbrace{ -\Big(\underbrace{(x-\frac{1}{2})^2 }_{+ve}+ \underbrace{\frac{11}{4}}_{+ve}\Big)}_{-ve}$
So, a positive value can never be equal to a negative value.
Hence, the equation does not contain any solution.
So, option $\mathbf B$ is the right answer.
GRAPHICAL SOLUTION:
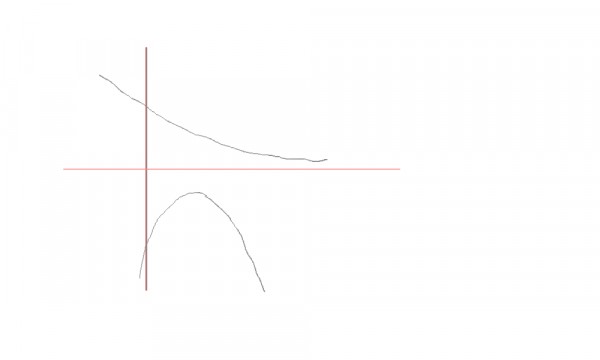
Above curves represent the graph of $a^x$ where $0 \lt x \lt1$ and the quadratic equation.
The quadratic equation is downward open parabola since the coefficient of $x^2$ is negative.
Vertex of the parabola is located at $x = \frac{-b}{2a} = \frac{1}{2}$
Also note that it will never intersect the $x-axis$ as its Discriminant, D is $-ve$
$D = b^2-4ac = 1^2-4(-1)(-3) = 1-12 = -11 \lt0$
Hence, the two curves will never intersect each other, which means no solution is possible to the given inequality.
$\therefore \mathbf B$ is the correct option.