The correct answer is option C.
Consider f(x) is a function that is twice continuously differentiable on an interval I. Then the function f(x) is
- convex if $f''(x)>0 ,$ for all x in I.
- concave if $f''(x)<0 ,$for all x in I.
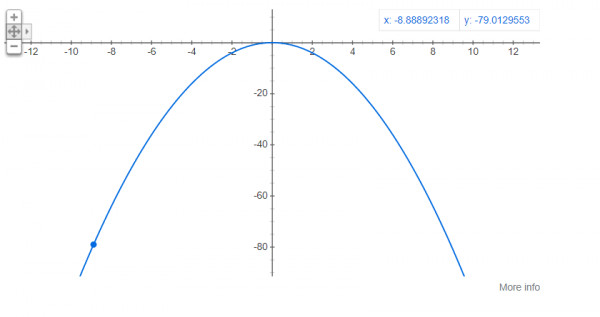
let take ,
$f(x)=-x^{2}$
This graph is a concave graph as
$f''(x)=-2<0$
Figure,
now ,
Let’s take $g(x)=e^{x}$ ,It is monotone increasing function.
Figure,

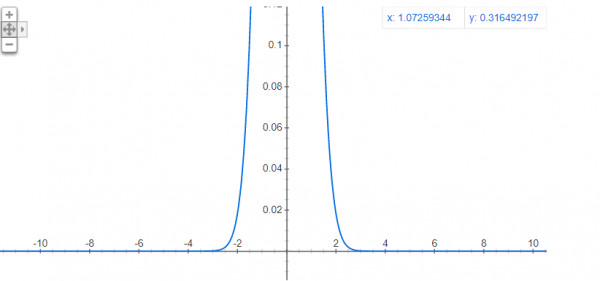
Now if we see $h(x)=g(f(x))=e^{-x^{2}}$
$h''(x)=2e^{-x^{2}}\left [ 2x^{2}-1 \right ]$.
It is concave when $-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}$ range
it is convex when $x>\frac{1}{\sqrt{2}}$ and $x<-\frac{1}{\sqrt{2}}$
Graph ,
As concaveness or convexnees we can find out by second differentiation .
As it is clear that it will never always concave or convex so option a and b is false.