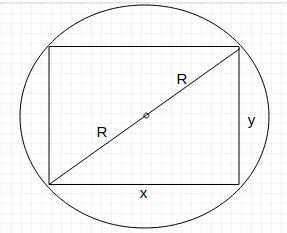
$(R+R)^2 = x^2 + y^2 \Rightarrow y^2 =4R^2 - x^2 $
Area of Rectange, $A = xy \Rightarrow A^2 = x^2y^2 = x^2(4R^2 - x^2) = 4R^2x^2 - x^4$
For area of largest rectange, $\frac{d(A^2)}{dx} = 0$
So, $8R^2x - 4x^3 = 0 \Rightarrow x=0, \pm\sqrt{2}R.$ Only $x=+\sqrt{2}R$ is possible.
For $x=\sqrt{2}R,$ $\frac{d^2(A^2)}{dx^2} <0$
So, at $x= \sqrt{2}R,$ the area of rectangle which is inscribed in a circle of radius $R$ is maximum.
Now, $y^2 =4R^2 - x^2 \Rightarrow y^2 = 4R^2 - 2R^2.$ So, possible value of $y$ is also $\sqrt{2}R.$
Hence, the area of the largest rectangle that can be inscribed in a circle of radius $R$ is : $\sqrt{2}R \times \sqrt{2}R = 2R^2 $
$\textbf{Edit:}$
Alternatively, we can take the help of Lagrangian Multiplier,
$\mathcal{L}= xy – \lambda( x^2 + y^2 – 4R^2)$
$\frac{\partial \mathcal{L}}{\partial x} = 0 \Rightarrow x = \frac{y}{2\lambda}$ and $\frac{\partial \mathcal{L}}{\partial y} = 0 \Rightarrow y = \frac{x}{2\lambda}$
So, $x=\pm y$ for $\lambda \neq 0$
$x^2 + y^2 = 4R^2 \Rightarrow x^2 + x^2 = 4R^2 \Rightarrow x^2 = 2R^2$
Hence, Area = $xy= x^2 = 2R^2$