Number of $a’s$ in $x$ are divisible by $2$ but not divisible by $3$ means number of $a's$ can be $2,4,8,10,14,16,20,22,26,\ldots$
Terms which are divisible by both $2$ and $3$ like $6,12,18,24,\ldots$ are dropped from the above sequence at finite interval in $*$ position from above sequence $2,4,*,8,10,*,14,16,*,20,22,*,26,28,*,32,34,\ldots$
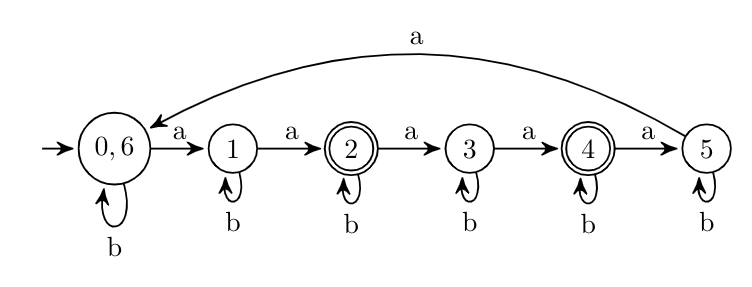
Here, sequence $\{6,12,18,24,\ldots\}$ is in AP. Now, to drop this sequence from our original sequence which represent the number of $a's$, we have to go through at least total $7$ states which says total $6$ $a's$ have seen so far and since terms of this sequence come at regular interval, So, we will make a cycle in the DFA as :

Now, observe that states $0$ and $6$ are equivalent because by definition, $2$ states $p$ and $q$ are equivalent i.e.
$p \approx q \overset{\textit{def}}\Leftrightarrow \forall x \in \Sigma^{*}(\hat{\delta}(p,x) \in F \Leftrightarrow \hat{\delta}(q,x) \in F)$
It says $2$ states are equivalent if for all strings, they both either go to final state or both go to non-final state means they have the same nature.
So, here, we can merge states $0$ and $6$. Other states can't be merged because they are in cycle and if we merge states which are in cycle, machine will not accept the desired number of $a's$ and reject $6,12,18,\ldots$ $a's.$
So, our final collapsing $\textsf{DFA}$ is :