Complement
Let M = < Q , ,q0 ,
,q0 ,  , A > be a DFA that accepts a language L.
, A > be a DFA that accepts a language L.
Then a DFA that accepts the complement of L, i.e.  * - L, can be obtained by swapping its accepting states with its non-accepting states, that is Mc = < Q ,
* - L, can be obtained by swapping its accepting states with its non-accepting states, that is Mc = < Q ,  , q0 ,
, q0 ,  , Q - A > is a DFA that accepts
, Q - A > is a DFA that accepts  * - L .
* - L .
For example the following DFA accepts the language a+ over  = { a , b }.
= { a , b }.
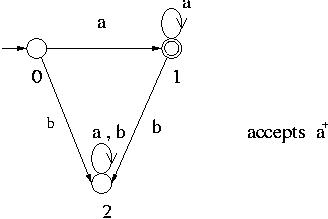
A DFA that accepts its complement is obtained from the above DFA by changing all single circles to double circles and vice versa as shown below.
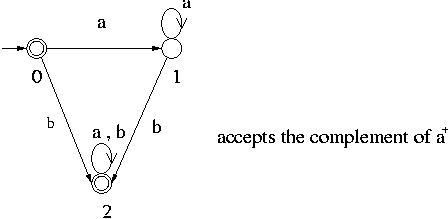
Remark 1: If we have NFA rather than DFA, we must first convert it to DFA before swapping states to get its complement.
Remark 2: Since a language is regular if and only if it is accepted by some NFA, the complement of a regular language is also regular.
So C is correct.
Ref: https://www.cs.odu.edu/~toida/nerzic/390teched/regular/fa/complement.html