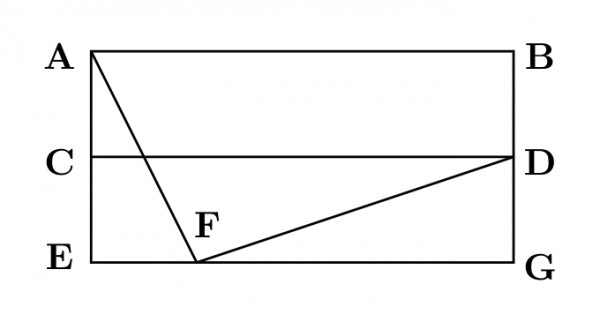
For the network given in the figure below, the routing tables of the four nodes $A$, $E$, $D$ and $G$ are shown. Suppose that $F$ has estimated its delay to its neighbors, $A$, $E$, $D$ and $G$ as $8$, $10$, $12$ and $6$ msecs respectively and updates its routing table using distance vector routing technique.
$$\overset{\textbf{Routing Table of A}}{\begin{array}{|c|r|}\hline
\text{A}&0\\ \hline
\text{B}&40\\ \hline
\text{C}&14\\ \hline
\text{D}&17\\ \hline
\text{E}&21\\ \hline
\text{F}&9\\ \hline
\text{G}&24\\ \hline
\end{array}}\qquad
\overset{\textbf{Routing Table of D}}{\begin{array}{|c|r|}\hline
\text{A}&20\\ \hline
\text{B}&8\\ \hline
\text{C}&30\\ \hline
\text{D}&0\\ \hline
\text{E}&14\\ \hline
\text{F}&7\\ \hline
\text{G}&22\\ \hline
\end{array}} \qquad
\overset{\textbf{Routing Table of E}}{\begin{array}{|c|r|}\hline
\text{A}&24\\ \hline
\text{B}&27\\ \hline
\text{C}&7\\ \hline
\text{D}&20\\ \hline
\text{E}&0\\ \hline
\text{F}&11\\ \hline
\text{G}&22\\ \hline
\end{array}}\qquad
\overset{\textbf{Routing Table of G}}{\begin{array}{|c|r|}\hline
\text{A}&21\\ \hline
\text{B}&24\\ \hline
\text{C}&22\\ \hline
\text{D}&19\\ \hline
\text{E}&22\\ \hline
\text{F}&10\\ \hline
\text{G}&0\\ \hline
\end{array}}
$$
- $$\begin{array}{|c|r|} \hline \text {A} & \text{8} \\\hline \text {B} & \text{20} \\\hline \text{C} & \text{17} \\\hline \text{D} & \text{12} \\\hline \text {E} & \text{10} \\\hline \text {F} & \text{0} \\\hline \text{G} & \text{6} \\\hline \end{array}$$
- $$\begin{array}{|c|r|} \hline \text {A} & \text{21} \\\hline \text {B} & \text{8} \\\hline \text{C} & \text{7} \\\hline \text{D} & \text{19} \\\hline \text {E} & \text{14} \\\hline \text {F} & \text{0 } \\\hline \text{G} & \text{22} \\\hline \end{array}$$
- $$\begin{array}{|c|r|} \hline \text {A} & \text{8} \\\hline \text {B} & \text{20} \\\hline \text{C} & \text{17} \\\hline \text{D} & \text{12} \\\hline \text {E} & \text{10} \\\hline \text {F} & \text{16} \\\hline \text{G} & \text{6} \\\hline \end{array}$$
- $$\begin{array}{|c|r|} \hline \text {A} & \text{8} \\\hline \text {B} & \text{8} \\\hline \text{C} & \text{7} \\\hline \text{D} & \text{12} \\\hline \text {E} & \text{10} \\\hline \text {F} & \text{0} \\\hline \text{G} & \text{6} \\\hline \end{array}$$