In a pushdown automaton $P=(Q, \Sigma, \Gamma, \delta, q_0, F)$, a transition of the form,
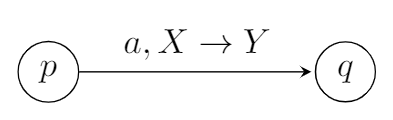
where $p,q \in Q$, $a \in \Sigma \cup \{ \epsilon \}$, and $X,Y \in \Gamma \cup \{ \epsilon \}$, represents $$(q,Y) \in \delta(p,a,X). $$Consider the following pushdown automaton over the input alphabet $\Sigma = \{a,b\}$ and stack alphabet $\Gamma = \{ \#, A\}$.
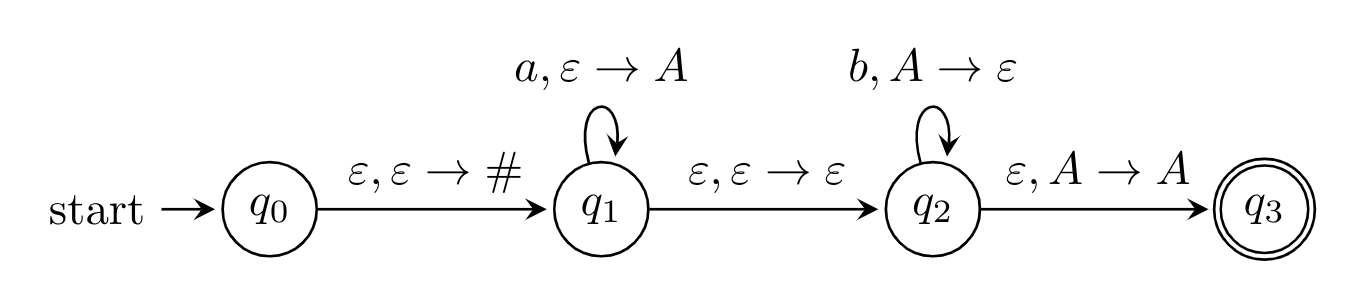
The number of strings of length $100$ accepted by the above pushdown automaton is ___________