
As per the option B it says root of T can be an articulation point in G if and only if it has 2 or more children, now here for simplicity I have taken simple case where root will have 2 children and I will tell you for the generalized case later. Also as its double implication lets see it as separately
Case 1: If root is articulation point then root will have 2 or more children
If a vertex is articulation point then its removal disconnects the graph into $2$ or more components means there must exist at least $2$ vertices for which each and every path in between them will pass through articulation point and removal of articulation point will destroy all the paths in between them and thereby disconnecting the graph into components, otherwise that vertex can not be an articulation point because even if we remove that vertex still every pair of vertices has some other path and hence graph wont get disconnected.
Now when we start DFS Traversal from vertex $V$ (articulation point) we may visit either the vertex from $G_1$ or $G_2$ first, lets say we visited vertex of $G_2$ first now during the DFS traversal which becomes child of $V$ now we can never visit any vertex in $G_1$ unless and until we do not use vertex $V$ because every path will go through vertex $V$ only, and by the nature of DFS no vertex during the traversal of sub-graph $G_2$ can visit the vertex $V$ again as it will be having Gray color/ not yet finished (refer DFS algorithm from CLRS for better understanding) and because of this property all the vertices in $G_2$ will be exhausted and we will be back to the vertex $V$ but vertex $V$ still has path to the unvisited vertices of sub-graph $G_1$ and hence the first vertex which will be visited in $G_1$ will become the new child of $V$ thereby making $2$ children for the root vertex $V$ which is the articulation point.
Case 2: If root vertex has 2 or more children then it is articulation point
Lets say in an undirected graph if root has $2$ children then it is true that there is no path between the vertices in left sub-tree and right sub-tree of vertex $V$ (w.r.t DFS traversal tree) because if there had been any path between the left and right sub-tree the in that case if we start with right child then before reaching to the root all the vertices in left sub-tree would have been visited and root had only single child but it is contradiction as root has $2$ children and hence there can be no path between the left and right sub-tree of vertex $V,$ thereby making it the ONLY vertex through which vertices in left and right sub-tree are connected
Hence above two cases proves the option B is correct and A is incorrect
For the generalized case visualize star graph with many vertices where center is articulation point, now you got the intuition and apply this on any graph!
Lets understand option C.
Option C says that leaf of tree $T$ can be an articulation point, its FALSE because if some vertex is leaf of tree $T$ then all the vertices to which it connects are already been visited which indicates that even without using this leaf vertex there exists path between all of its neighbors and hence it can not be an articulation point.
Hence option C is incorrect
Now option D
Option D talks about ancestors and decedents $X$ and $Y$ and says that if $X$ is ancestor of $U$ in $T$ and $Y$ is decedent then all the paths between $X$ and $Y$ must pass through $U$ but we have counter for this as shown below.
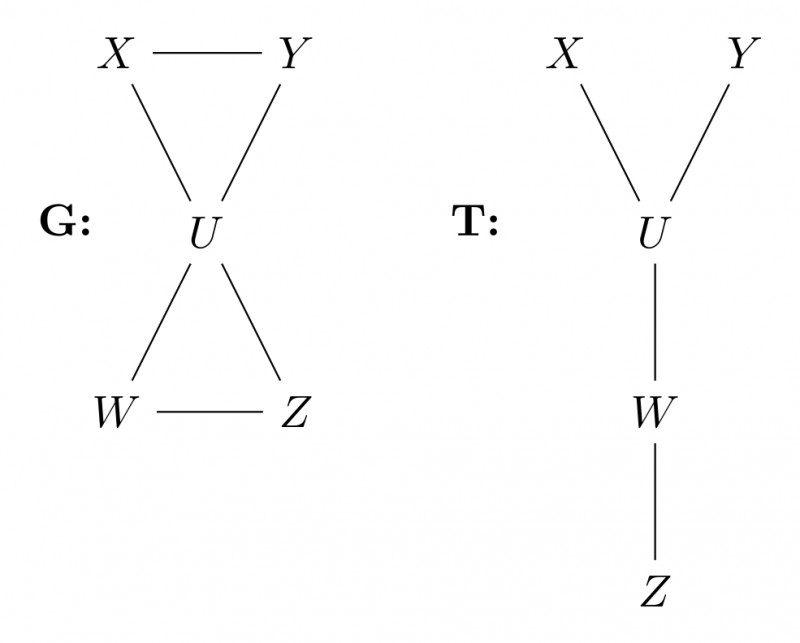
Hence option D is incorrect