GATE CSE 2021 Set 1 | Question: 17

Question

Consider the following undirected graph with edge weights as shown:

The number of minimum-weight spanning trees of the graph is ___________.

Answer 1

For finding a minimum-weight spanning tree we have different algorithms like the Prim, Kruskal’s algorithm.

A spanning tree means a sub-graph of the original graph that should be the tree and connected to all the vertices together.

A Minimum spanning tree is for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of the weights of each edge of the spanning tree.

Now to find out MST of the given graph using Kruskal’s algorithm (we can use any method here) we can follow the 2 step process:

1. Sort all the edges in increasing order of their weight. 
2. Select the smallest edge & check if it forms a cycle with the spanning tree formed so far. If a cycle is not formed, include this edge. Else, discard it. 

After applying the above steps graph will look like this:

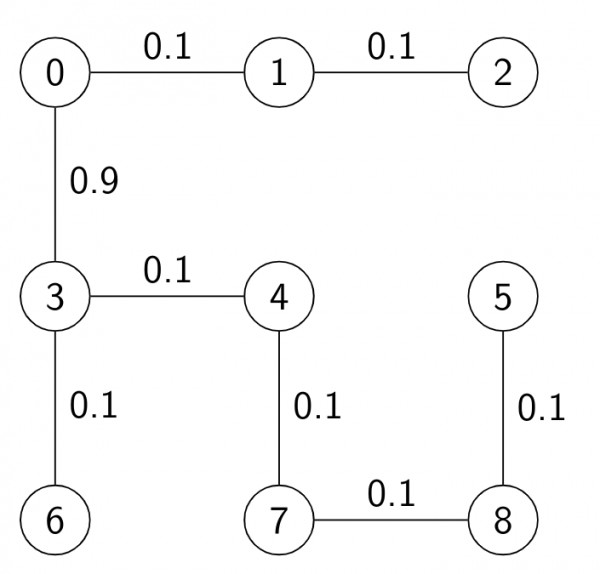
In the above figure, we cannot add edges $(6,7)$ or $(4,5)$ because it creates a cycle in MST. So we have only $3$ edges remaining which are $(0,3),(1,4)$ and $(2,5).$

Since we know that for $n$ vertices, the number of edges should be $(n-1)$ in MST. so from 3 edges we can select only $1$ edge that is :

$\binom{3}{1}= 3$  ways. 

• $1^{st} MST$

  

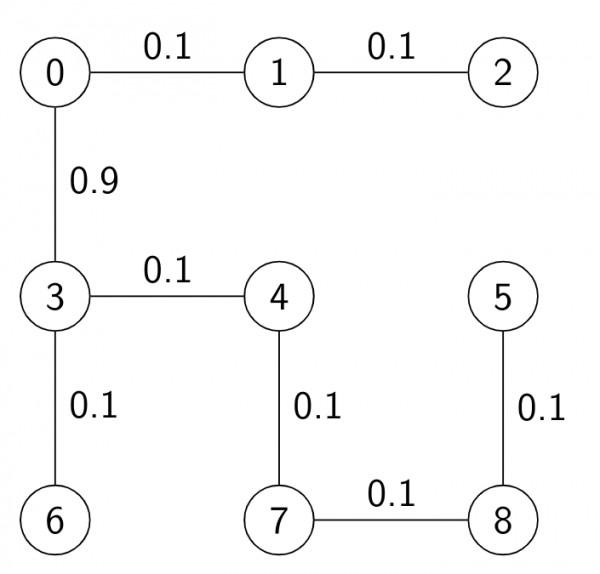
•  $2^{nd} MST:$

  

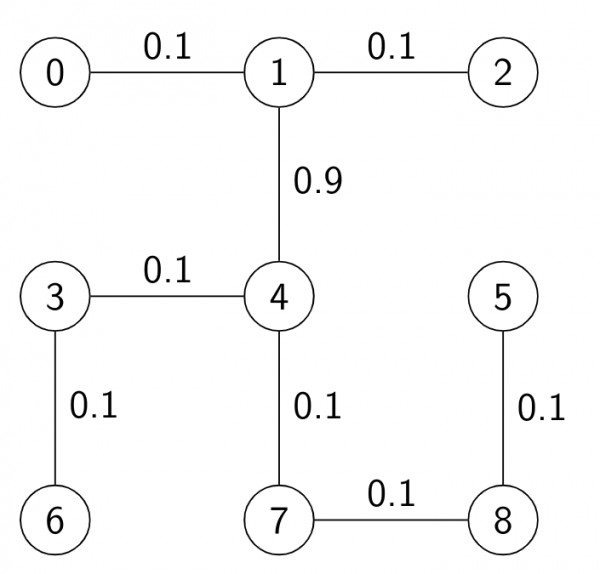
• $3^{rd} MST:$

  

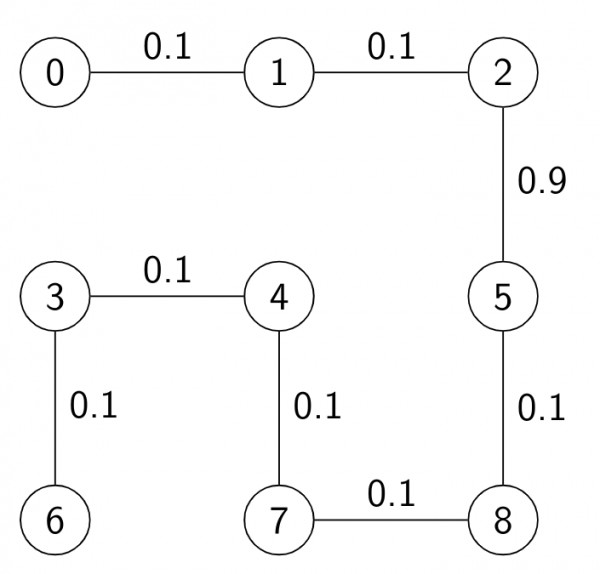
$\therefore$ Total $3$ MSTs are possible for the given graph.

For more Refer here:Kruskal Algorithm

Answer 2

First include all 0.1 edges,  only three mst possible

Answer 3

ANS IS 3. 

AFTER SELECTING ALL THE EDGES OF WEIGHT 0.1 WE HAVE 3 POSSIBILITY TO SELECT ONE EDGE OF WEIGHT 0.9.