Consider a computer network using the distance vector routing algorithm in its network layer. The partial topology of the network is shown below.
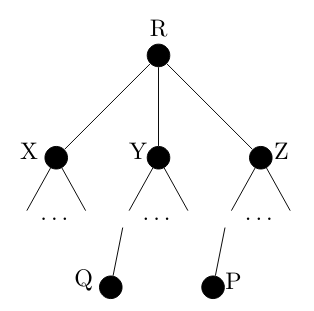
The objective is to find the shortest-cost path from the router $R$ to routers $P$ and $Q$. Assume that $R$ does not initially know the shortest routes to $P$ and $Q$. Assume that $R$ has three neighbouring routers denoted as $X$, $Y$ and $Z$. During one iteration, $R$ measures its distance to its neighbours $X$, $Y$, and $Z$ as $3$, $2$ and $5$, respectively. Router $R$ gets routing vectors from its neighbours that indicate that the distance to router $P$ from routers $X$, $Y$ and $Z$ are $7$, $6$ and $5$, respectively. The routing vector also indicates that the distance to router $Q$ from routers $X$, $Y$ and $Z$ are $4$, $6$ and $8$ respectively. Which of the following statement(s) is/are correct with respect to the new routing table o $R$, after updation during this iteration?
- The distance from $R$ to $P$ will be stored as $10$
- The distance from $R$ to $Q$ will be stored as $7$
- The next hop router for a packet from $R$ to $P$ is $Y$
- The next hop router for a packet from $R$ to $Q$ is $Z$