GATE CSE 2021 Set 2 | Question: 12

Question

 

Let $L_1$ be a regular language and $L_2$ be a context-free language. Which of the following languages is/are context-free?

• A. $L_1 \cap \overline{L_2} \\$
• B. $\overline{\overline{L_1} \cup \overline{L_2}} \\$
• C. $L_1 \cup (L_2 \cup \overline{L_2}) \\$
• D. $(L_1 \cap L_2) \cup (\overline{L_1} \cap L_2)$

Comments

Answer 1

The options should be $b,c,d$. 

Options –

(a) The Complement of CFL is Recursive. The intersection of Recursive and Regular is Recursive.

(b) It is $L_1 \cap L_2$ and intersection of CFL and regular is CFL.

(c)It is $\sum$ itself as $L_2  \cup \bar{L_2}$ is $\sum$ and union of $\sum$ and $L_1$ is $\sum$ which is regular and thus CFL.

 (d) Solving this you will get $L_2$ which is CFL. See the image below.

​​​​​​​

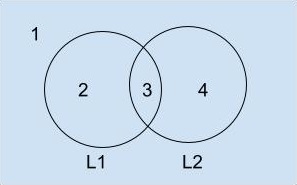
We can write the $(d)$ option as,

$= (23 \cap 34) \cup (14 \cap 34)$

$= (3) \cup (4)$

$= L_2$

Comments

in option D both are CFL ( regular intersection with CFL)   union of two CFL is CFL

Answer 2

Given : $L_1$= Regular language

$L_2$=CFL

     A) $L_1\cap \bar L_2$: as we know that CFL is not closed under complement operation. CFL complement is REC.

           therefore Reg  $\cap$ $\overline{CFL}$ =REC which is not CFL.

           hence option A is wrong here.

     B)  $\overline{(\bar L_1\cup \bar L_2)}$: this can be written as $\overline{\overline{L_1}}\cap\overline{\overline{L_2}}\implies L_1\cap L_2$.

           hence Regular $\cap$ CFL is CFL because CFL is closed with regular intersection.

            option $B$ is correct.

     C) $L_1\cup(L_2\cup \bar L_2)$: CFL complement is REC language.

           CFL$\cup$ REC is REC language and union with regular language is REC which is not CFL.

          so option $C$ is false here.

     D) $(L_1\cap L_2)\cup(\bar L_1\cap L_2)$; This can be written as:

          (regular $\cap$ CFL)$\cup$( Regular $\cap$ CFL)

         $\implies$ (regular $\cap$ CFL)= CFL, (Regular $\cap$ CFL)=CFL

        $\implies$ CFl$\cup $CFL=CFL 

Option $D$ is correct.

$\therefore$ Option $B$ and $D$ is correct.

Ref: closure-property-of-language-families

Comments

@Hira C is given as CFL in official key but I totally agree with you reasoning. @Arjun Sir can you please shed some light here?

Answer 3

B,C,D
 

---

Some insights beforehand:

 

Not Closed under Intersection:

$L_1=\{a^nb^*c^n\},L_2=\{a^nb^nc^*\}$ , $L_1\cap L_2=\{a^nb^nc^n\}$ not a CFL

 

Closed under Union:
Let both of these CFLs be represented using grammars with start symbols $S_1$ and $S_2$, we define a new symbol $S^{’}$ such that $S^{’}\to S_1/S_2$ note, we definitely have a NPDA but could be represented under DPDA if the language allows it to be(2 RLs).

 

Not Closed under Complementation:

$L_1\cap L_2=\overline{\overline{L_1}\cup\overline{L_2}}$

We know that intersection isn’t  closed under context free languages and union is closed under CFL(NPDA) so it must be the case that complementation isn’t closed under CFL.
Example: $L=\{a^nb^nc^n\}$ not a CFL but, $\overline{L}$ is and infact can be solved using a NPDA.

 

Intersection and Union of a CFL is RL is CFL.

---

Now,

• A. $L_2$ is complemented so, needn’t be a CFL.

• A. $\overline{\overline{L_1}\cap\overline{L_2}}=L_1\cup L_2$ union of a CFL and RL is a CFL
• B. $L_1\cup(L_2\cup\overline{L_2})=L_1\cup(\Sigma^*)=\Sigma^*$  hence a CFL.
• C. $(L_1\cap L_2)\cup(\overline{L_1}\cap L_2)=L_2$  or it’s a union of two CFLs if you don’t bother to solve.

---