Given statements are,
- $\text{Statement 1}:$ All entrepreneurs are wealthy.
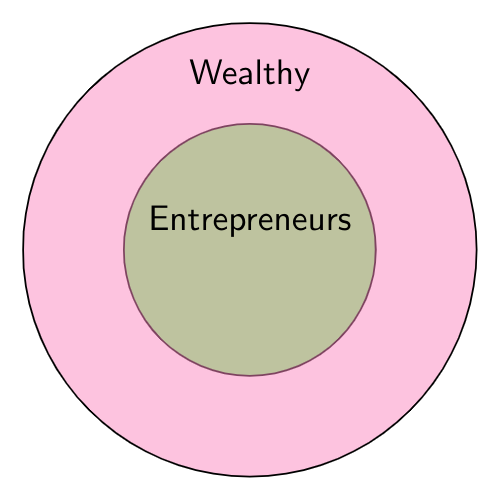
- $\text{Statement 2}:$ All wealthy are risk seekers.
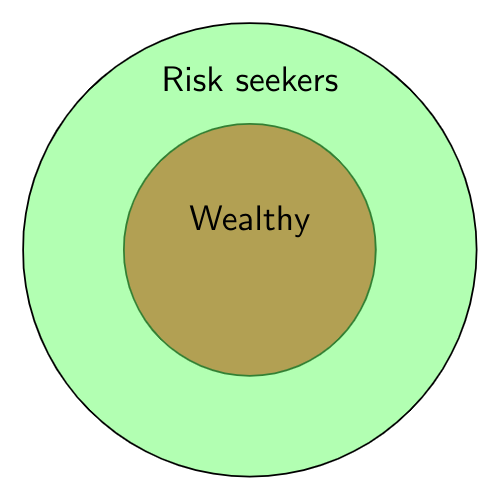
- $\text{Conclusion I}:$ All risk seekers are wealthy.
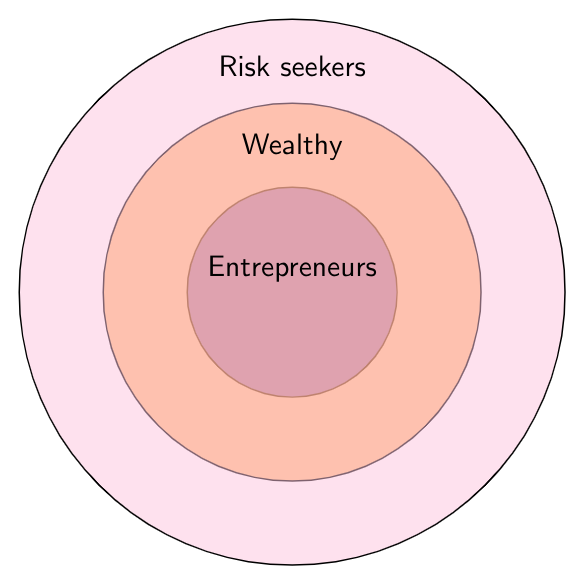
From the above Venn diagram, not all risk seekers are wealthy. So, $\text{conclusion I}$ is false.
- $\text{Conclusion II}:$ Only some entrepreneurs are risk seekers.
From the above Venn diagram, all entrepreneurs are risk seekers. So, $\text{conclusion II}$ is also false.
So, the correct answer is $(C).$