Let the side of the square be $1\;\text{cm},$ then $r = 1\;\text{cm}.$
From the center $S,$ we can draw the circle, and only the quarter part is shown in the figure.
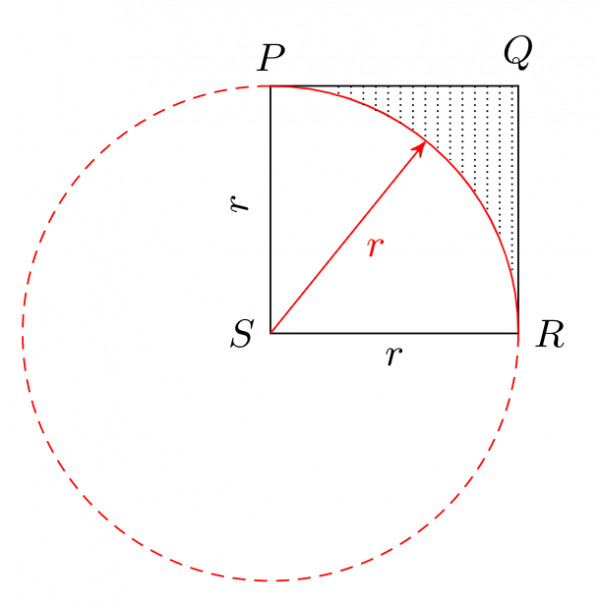
The shaded area $A_{1} = A_{\text{square}} – A_{\text{quarter circle}} = 1 – \dfrac{\pi}{4}$
From the center $Q,$ we can draw the circle, and only the quarter part is shown in the figure.
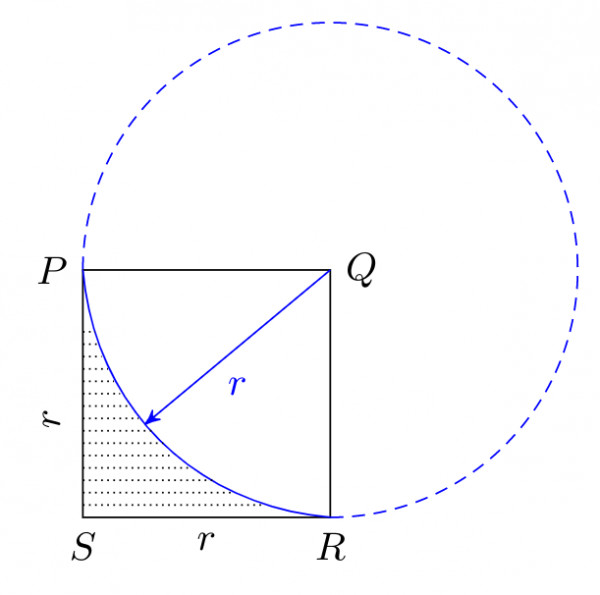
The shaded area $A_{2} = A_{\text{square}} – A_{\text{quarter circle}} = 1 – \dfrac{\pi}{4}$
Now, we can combine the above two figures, we get,

Now, the shaded area $ = A_{\text{square}} – A_{1} – A_{2}$
$\quad = 1 – \left(1-\dfrac{\pi}{4}\right) – \left(1-\dfrac{\pi}{4}\right)$
$\quad = – 1 + \dfrac{2\pi}{4} = \dfrac{\pi}{2} – 1$
Now, the required probability $ = \dfrac{\text{Favorable shaded area}}{\text{Total area}} = \dfrac{\frac{\pi}{2} – 1}{1} = \dfrac{\pi}{2} – 1.$
$\therefore$ The probability that any point picked randomly within the square falls in the shaded area $ = \dfrac{\pi}{2} – 1.$
So, the correct answer is $(C).$