Method 1(Complete Analysis) :
Directed Spanning Tree definition is given. From the definition, it can be seen that Directed Spanning Tree(DST) is basically a Directed Acyclic Graph(DAG) whose root node is $5,$ and it contains all the vertices. We need to find how many such DAGs are possible. Let’s find out :
$5$ is the root node of the DAG. Let’s fix this at one place and permute all other numbers.
$5, 4, 3, 1, 2$ is one permutation possible, Similarly $5, 3, 4, 1, 2$ is other permutation possible.
Total there are $4! = 24$ permutations possible.
Now you give me any permutation (where $5$ is fixed at start) and I will give you corresponding DAG.
I will use one idea – $\color{blue}{ \text{ Connect a node to the nearest larger node on its left side. } }$
For example, you give me $5, 3, 4, 1, 2$ as permutation then i will draw following DAG.
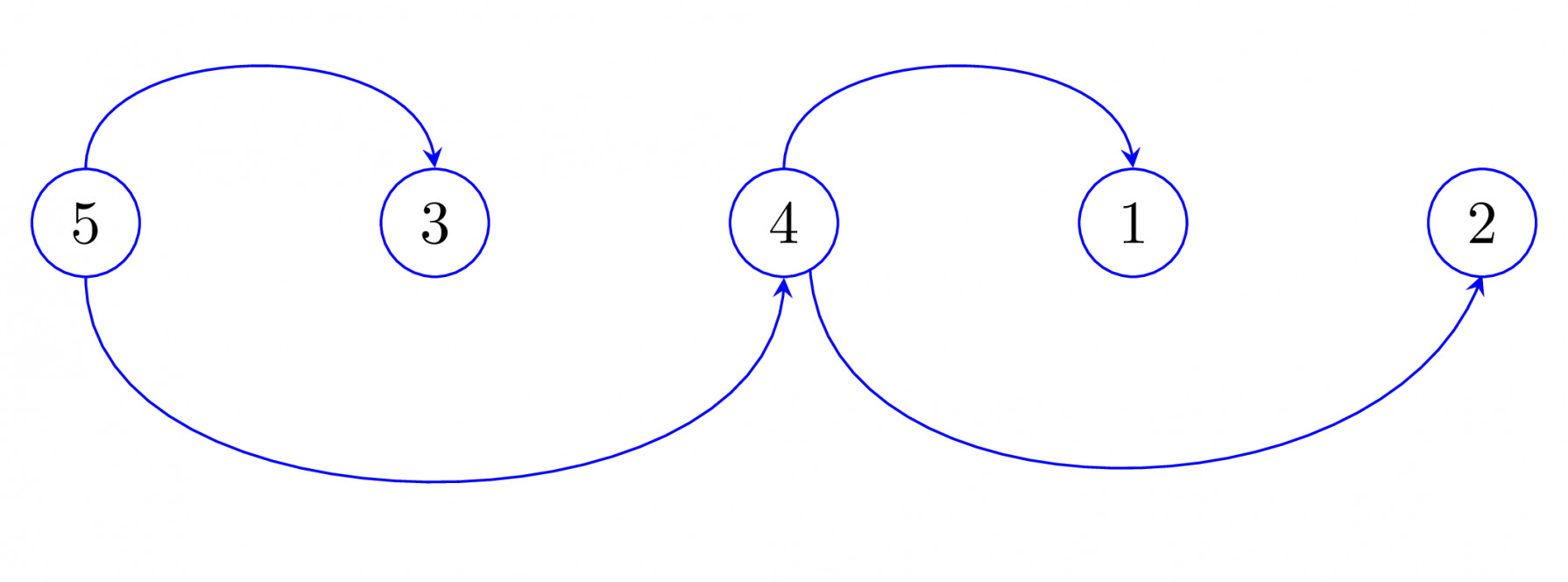
For $3$, nearest larger node on the left is $5$.
For $4$, nearest larger node on the left is $5$.
For $1$, nearest larger node on the left is $4$.
For $2$, nearest larger node on the left is $4$.
In this way, we can say that for every permutation there is $\color{red}{\text{unique }}$DAG.
Now, we can say number of DAGs is atleast as large as number of permutations. Maybe more DAGs than $4!$?
Can we have unique permutation for any given DAG ? – if yes then there is bijection between set of DAGs possible and the set of permutations possible, And So answer will be $4!$.
Before that first understand that these 2 DAGs are the same –
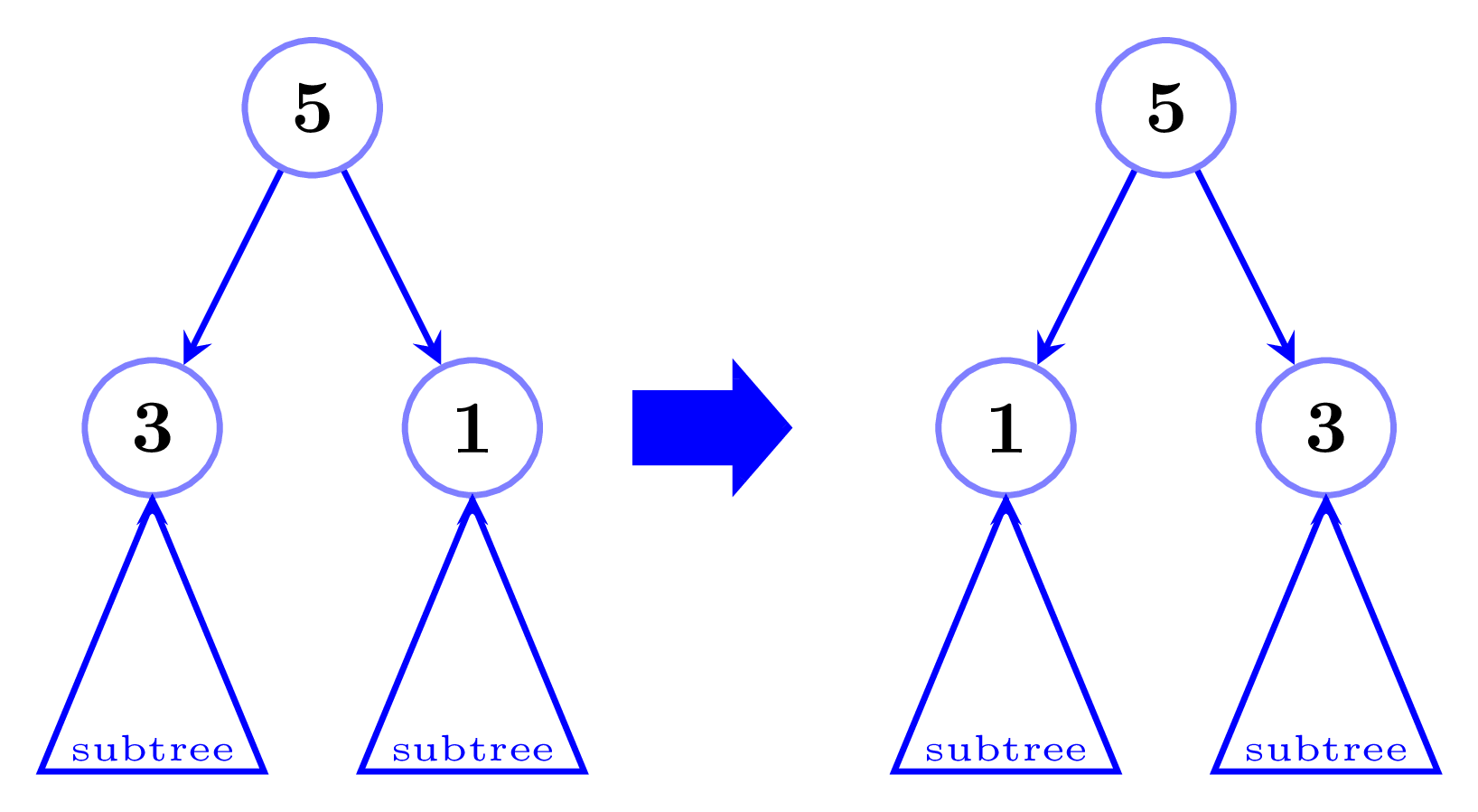
it does not matter if you swap left or right subtrees because they(Question makers) are interested in subgraphs and both the DAGs above are the same subgraph.
Now you give me a DAG, I will arrange all siblings of a node in increasing order(from left to right) and then I will take level order traversal to write permutation. For example, You give me the following DAG –
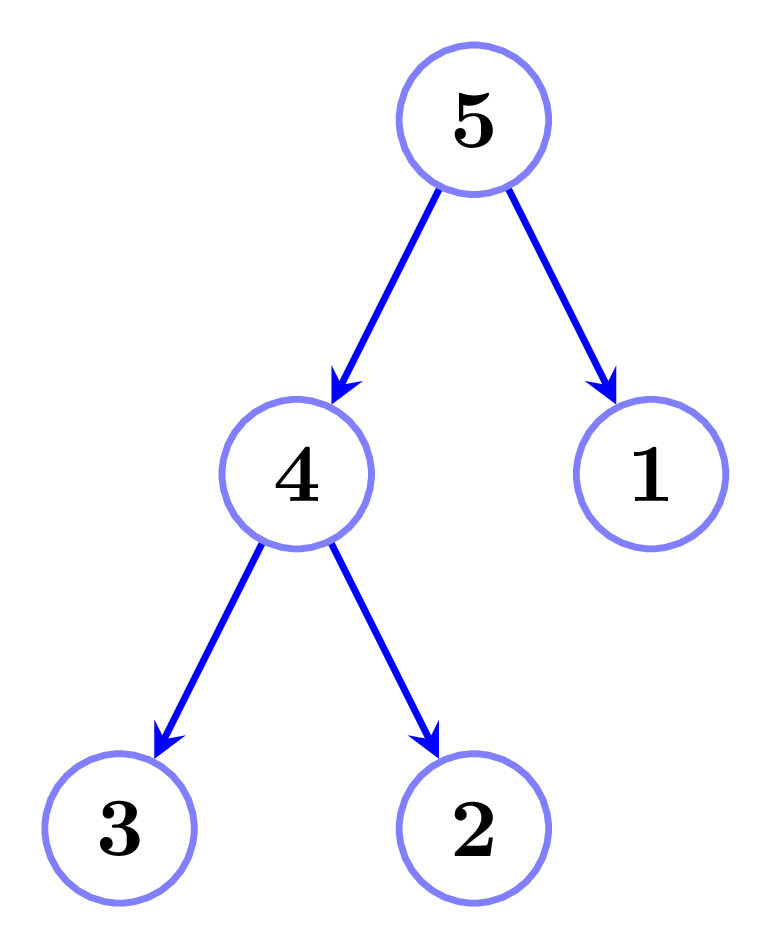
I will rearrange nodes as following –

Level order will be $5, 1, 4, 2, 3$
Now if we try to draw a DAG using same permutation, you will find same DAG.
For $1$, nearest larger node on the left is $5$.
For $4$, nearest larger node on the left is $5$.
For $2$, nearest larger node on the left is $4$.
For $3$, nearest larger node on the left is $4$.
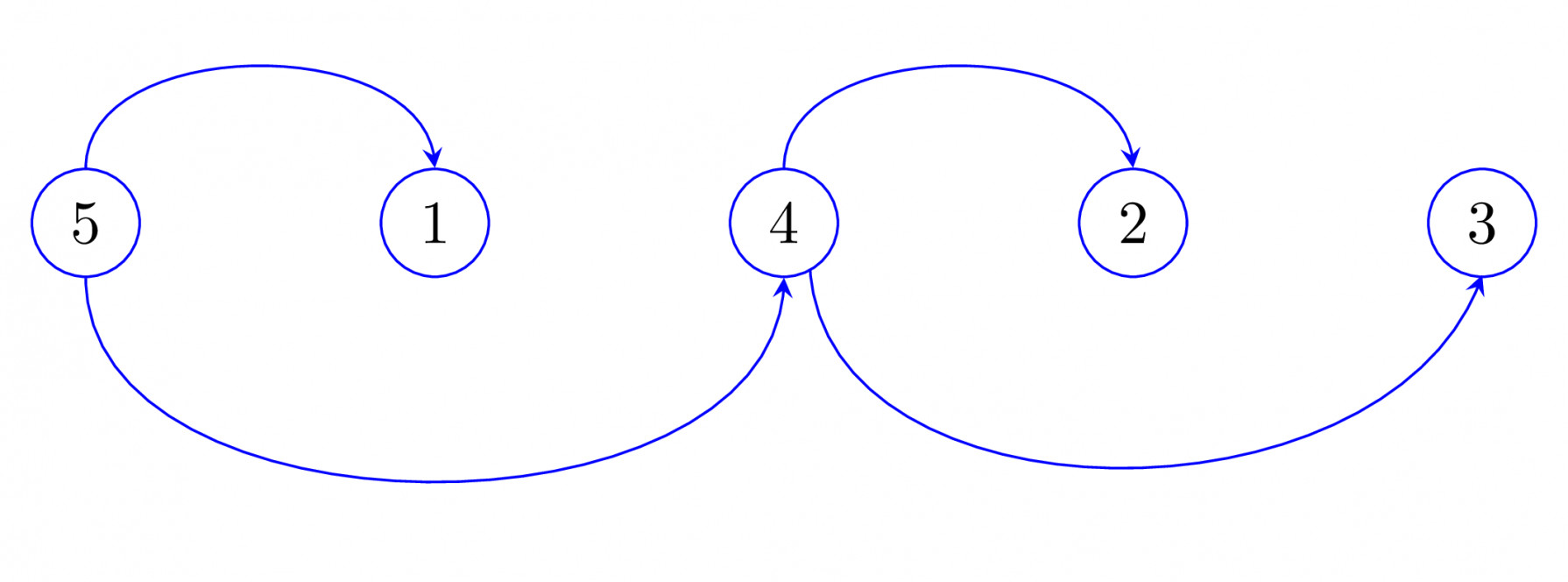
Both DAGs are the same.
Now it does not matter how I am converting a DAG to permutation or permutation to DAG. Consider my method as blackbox, I have some definite rule as blackbox and I can convert to each other uniquely.
So, we have shown that There is a bijection between set of DAGs possible and the set of permutations possible, Hence, answer will be $4!.$
Method 2 (Counting based on number of levels) : Will be added soon.