Answer : $0.5$
Once Q-R fails then Q will immediately update its distance to R to $\infty$. But P will still be having some finite value (which is 2).
Now it depends on P and Q, who is sending distance vector first.
if Q sends then system becomes stable immediately but if P sends first then it will be count to infinity. Please understand that count to infinity is not some wrong thing, it is just it takes some time to stable.
Since it is given in question that both have same average rate hence probability is also $\frac{1}{2}$ that P sends first than Q. Hence the answer.
But we can calculate answer more mathematically considering that time is continuous variable.
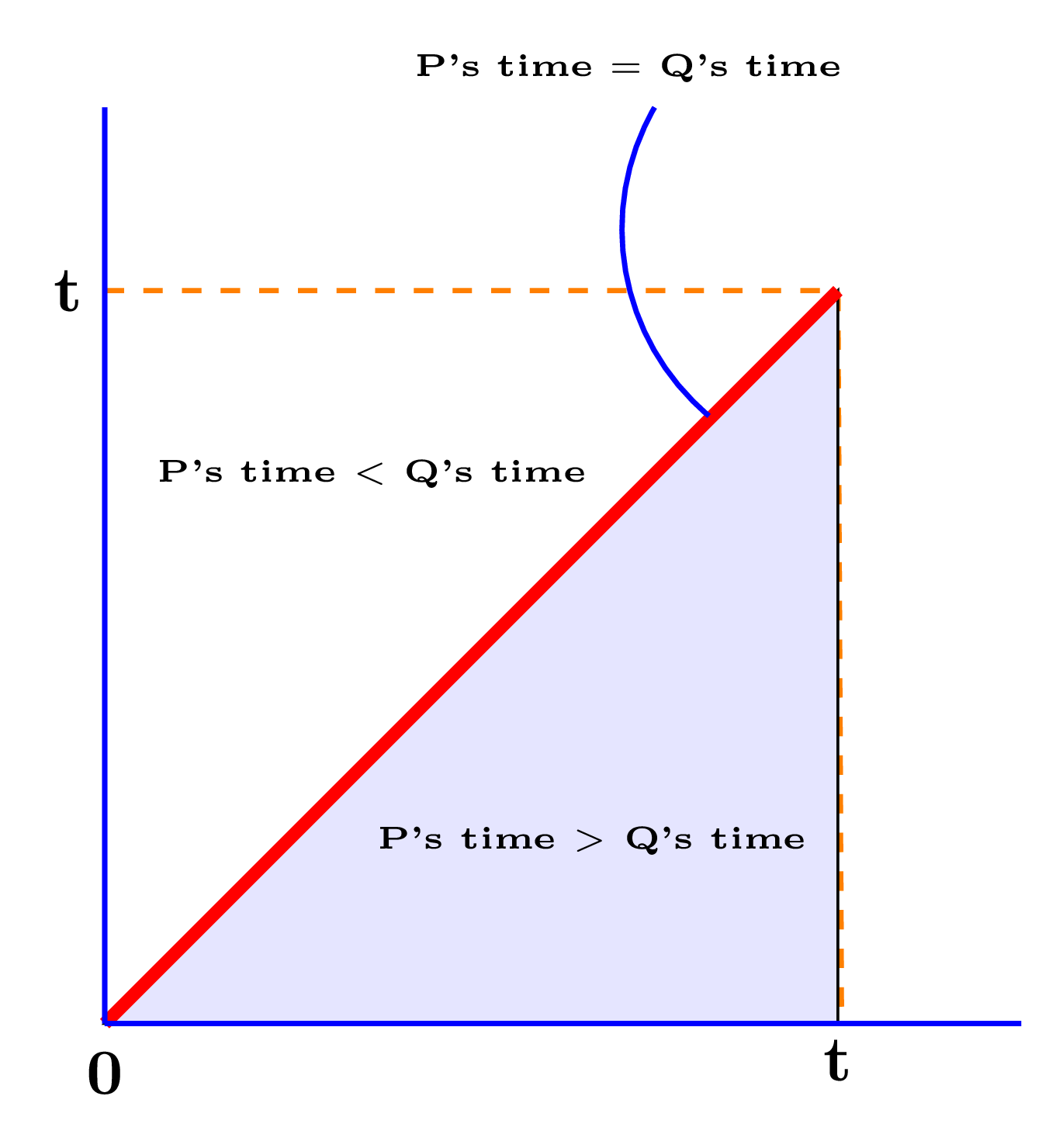
We are interested in probability represented by the shaded area,
which will be = $\frac{\text{Area of Tringle}}{\text{Area of Square}} = \frac{\frac{1}{2}t^2}{t^2} = \frac{1}{2}$
$\text{Method 2 OPTIONAL}$
Let $X$ and $Y$ be uniform random variables in $[0,t]$ representing time for $P$ and $Q$ respectively.
We need to find $P(X<Y) = ?.$
$P(X<Y) = P(X \leq Y) = P(X \leq k)$ (Let $Y =k$).
$ P(X \leq k) =$ Can you continue from here ?.
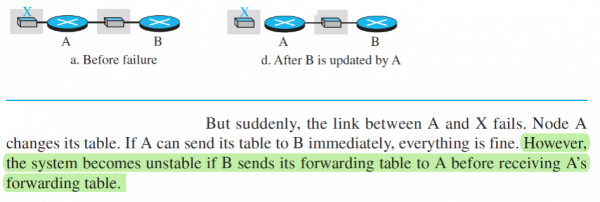
Also refer Forouzan snapshot of count to infinity
Similar question – [page 22, 23] https://www.classes.cs.uchicago.edu/archive/2003/winter/54001-1/data/hw2sol.pdf