Answer : A,B,C
In the given undirected weighted graph, All the edge weights are distinct, hence, there will be Exactly One Minimum Spanning Tree for the graph.
Option A :
The edge with the second smallest weight is always part of any minimum spanning tree of $G$.
Since $G$ has Exactly One MST, the above statement can be written as “The edge with the second smallest weight is always part of the minimum spanning tree of $G$.”
This can be proven by “Kruskal Algorithm” to find MST. Minimum Edge, Second Minimum Edge, both will be added in the MST by Kruskal Algorithm (Two edges cannot bring cycle)
Option B :
One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.
Since $G$ has Exactly One MST, the above statement can be written as “One or both of the edges with the third smallest and the fourth smallest weights are part of the minimum spanning tree of $G$.”
This is True. Minimum Edge, Second Minimum Edge, both will be added in the MST by Kruskal Algorithm (Two edges cannot bring cycle), BUT third minimum edge might introduce cycle in the MST, and if so happens, we do not include third minimum edge in the MST and add fourth minimum edge in the MST.
Option D :
$G$ can have multiple minimum spanning trees : False (Because all edge weights are distinct)
Option C :
Suppose $S \subseteq V$ be such that $S \neq \phi$ and $S \neq V$ . Consider the edge with the minimum weight such that one of its vertices is in $S$ and the other in $V- S $ . Such an edge will always be part of any minimum spanning tree of $G.$
This is True. This is a popular and basic property of Minimum Spanning Tree, known as “Cut Property.” The cut property is the basis for the algorithms that we consider for the MST problem. “Cut Property” and “Cycle Property” are basic theorems in the study of MST, and must be understood by all, with proof.
$\color{red}{\text{ Cut property }}$ :
Given any cut in an edge-weighted graph (with all edge weights distinct), the crossing edge of minimum weight is in the MST of the graph.
Given a cut $(S, V-S)$ of $G$, recall that an edge $(u, v) \in E$ is said to cross the cut if exactly one of $u$ and $v$ is in $S$. An edge $e = (u, v)$ is a minimum weight edge crossing the cut $(S, V-S)$ if its weight is the smallest of any edge crossing $(S, V-S).$
Then $e = (u,v)$ must be included in the minimum spanning trees of $G.$
Let $G = (V, E, w)$ be a connected undirected weighted graph with distinct edge weights. For any cut $(U,V-U)$ of G, the minimum weight edge that crosses the cut is in the minimum spanning tree $MST(G)$ of $G.$
We can prove it as following :
$\color{blue}{\text{ Proof :}}$
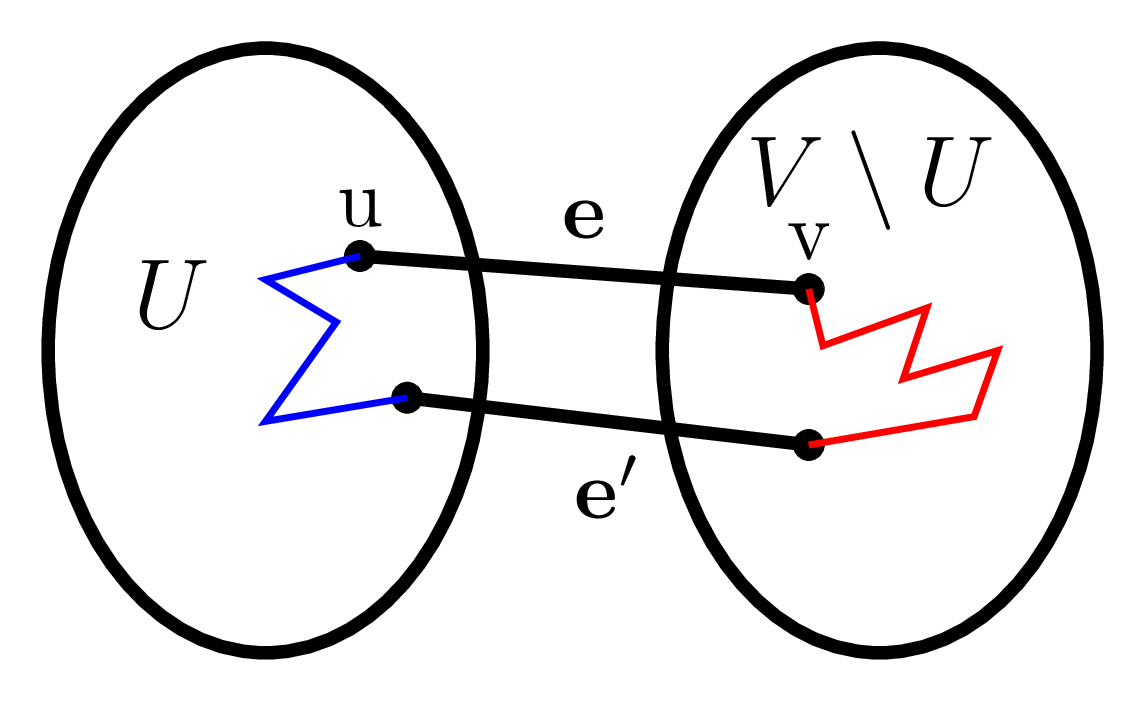
The proof is by contradiction. Assume the minimum-weighted edge $e = (u, v)$ is not in the MST. Since the MST spans the graph and is a connected tree, there must be a unique simple path $P$ connecting $u$ and $v$ in the MST (i.e., consisting of just edges in the MST). The path must cross the cut between $U$ and $V - U$ at least once since $u$ and $v$ are on opposite sides. Let $e’$ be an edge in $P$ that crosses the cut. By assumption the weight of $e’$ is larger than that of $e$. Now, insert $e$ into the graph—this gives us a cycle that includes both $e$ and $e’$—and remove $e’$ from the graph to break the only cycle and obtain a spanning tree again. Now, since the weight of $e$ is less than that of $e’$ , the resulting spanning tree has a smaller weight. This is a contradiction and thus $e$ must have been in the tree.
Hence Proved.
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2012/assignments/MIT6_046JS12_ps2_sol.pdf
https://algs4.cs.princeton.edu/43mst/
http://www.cs.cmu.edu/afs/cs/academic/class/15210-s15/www/lectures/mst-notes.pdf
$\color{red}{\text{ Cycle property :}}$ Let $G$ be a connected undirected weighted graph in which All edge weights are distinct.
Let $C$ be any cycle in $G$, and let $f$ be the max cost(weight) edge belonging to $C.$ Then the MST does not contain $f.$
https://www.cs.princeton.edu/courses/archive/spr07/cos226/lectures/mst.pdf
http://www2.hawaii.edu/~janst/311_f19/Notes/Topic-17.html
https://stackoverflow.com/questions/53057955/is-the-cut-property-two-way