Answer A
Suppose you are given a linkedlist like this –

And you want to convert this to as follows-
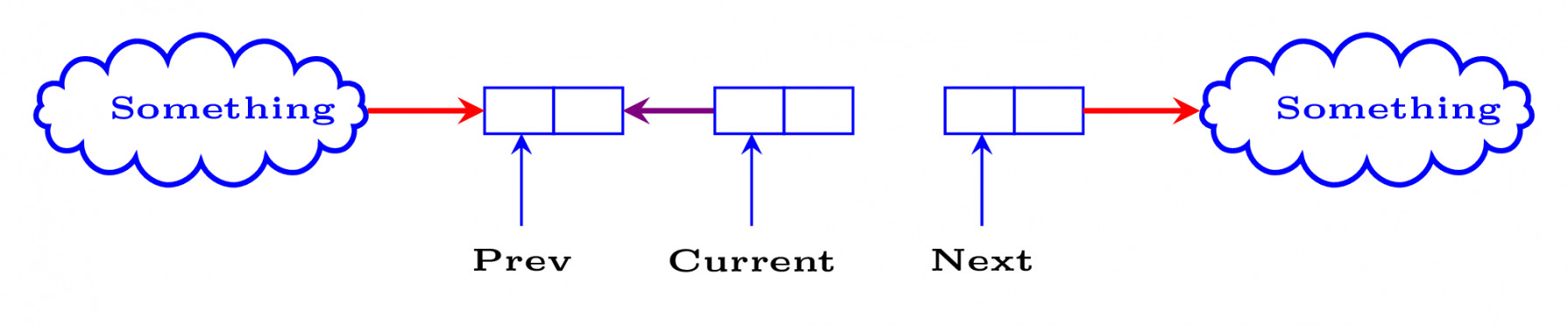
Which means, you just want to change pointer of node that is pointed by current.
Which line would do same ?
current->next = previous
That is all.
Now we just need to shift our pointers – prev, current and next.
Which is also easy
prev = current
current = next
next = current->next // or next = current->next
Now lets combine all lines together –
struct node * reverse( struct node * head )
{
struct node * prevP = NULL;
struct node * nextP = head->next;
while(head != NULL) {
head->next = prevP;
prevP = head;
head = nextP;
if(head) nextP = head->next;
}
return prevP;
}
Time complexity – $\theta(n)$
Space Complexity – $O(1)$
Full working code –
#include<stdio.h>
#include<stdlib.h>
struct node {
int data;
struct node *next;
};
typedef struct node Node;
struct node *createNode(int val){
struct node *newNode = malloc(sizeof( struct node ));
newNode->data = val;
newNode->next = NULL;
return newNode;
}
struct node* createListFromArray(int arr[], int arraySize)
{
struct node *rootNodePtr = createNode(arr[0]);
struct node *lastNodePtr = rootNodePtr;
for(int i = 1 ; i < arraySize; i++)
{
struct node *nodePtr = createNode(arr[i]);
lastNodePtr->next =nodePtr;
lastNodePtr=lastNodePtr->next;
}
return rootNodePtr;
}
void printlist(struct node *head){
printf("LIST:\n");
while(head!=NULL){
printf("%d ",head->data);
head = head->next;
}
printf("\n");
}
struct node * reverse( struct node * head )
{
struct node * prevP = NULL;
struct node * nextP = head->next;
while(head != NULL) {
head->next = prevP;
prevP = head;
head = nextP;
if(head) nextP = head->next;
}
return prevP;
}
int main()
{
int arr1[] = {55,10,2,3,4,20,7,6,8,9,12,15};
struct node *head =createListFromArray(arr1, sizeof(arr1)/sizeof(int));
printlist(head);
printlist(reverse(head));
}