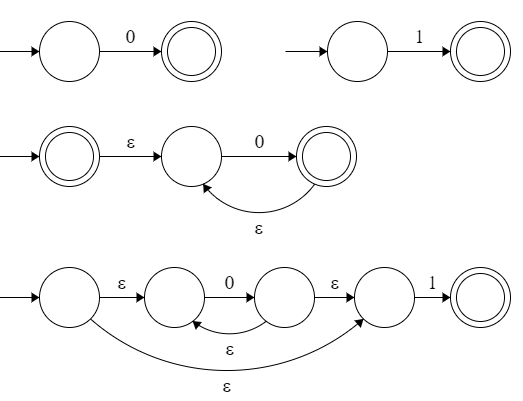
Convert the following regular expression (0+11)0*1 to NFA with e-transitions using the procedure given on pg. 66-67 Theorem 1.54 (Lemma 1.55) of the Introduction to Theory of Computation 3rd edition book by Michael Sipser.
I followed the example in the book, but what confuses me is when the Kleene star is added individually like 0*, how would we illustrate this?
This was my approach for just 0*1 part: