Option is C.
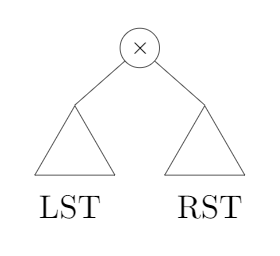
P: # elements in RST
$\Rightarrow$ Depending on $X,$ some number will go LST $\notin$ RST
$\Rightarrow$

Remaining elements for LST: $n- (p+1)$
$\underbrace{1,2,\ldots,n-(p+1)}_{\text{LST}\\n-(p+1)\\ \text{elements}}\qquad \underbrace{n-p}_{\text{Root}\\1\\ \text{element}}\qquad \underbrace{(n-p)+1,\ldots,n}_{\text{RST}\\p\\ \text{elements}}$