
Probability on each branch $= x = \frac{1}{2}$
2nd toss onwards, each toss layer gives us two success. (i.e. HH event or TT event )
$$\begin{align} E &= \sum k.p(k) \\ &= 2.(2x^2) + 3.(2x^3) + 4.(2x^4) + 5.(2x^5) + ... \\ &= 2.\left [ 2x^{2} + 3x^{3} + 4x^{4} + 5x^{5} + .... \right ] \\ &= 2.\left [ \frac{x}{(1-x)^2 } - x \right ] \\ \\ &\text{ putting x = } \frac{1}{2} \ \ \text{ ;}\\ \\ &= 2.\left [ \frac{\frac{1}{2}}{\left(\frac{1}{2}\right )^2} - \frac{1}{2} \right ] \\ &=3 \end{align}$$
A very similar QS :
An unbiased coin is tossed repeatedly and outcomes are recorded. What is the expected no of toss to get HT ( one head and one tail consecutively) ?
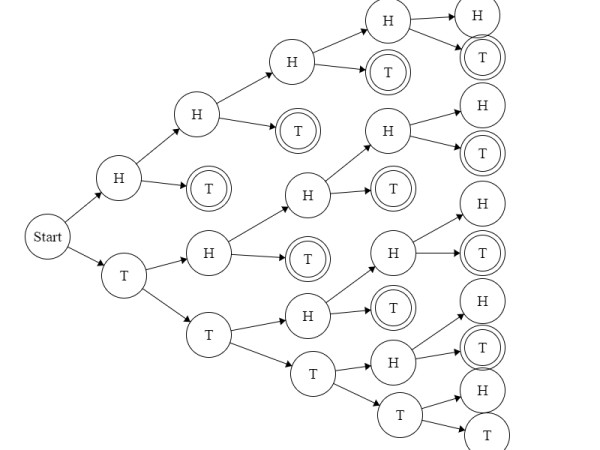
Probability in each branch $=0.5$. I double circled the satisfying toss events.
While observing the diagram I noticed that, from 2nd toss onward our required event starts showing up. Additionally,
1. in the $\text{2nd}$ toss (or the 3rd level) we have one satisfying case.
2. in the $\text{3rd}$ toss (or the 4th level) we have two satisfying case.
3. in the $\text{4th}$ toss (or the 5th level) we have three satisfying case.
4. in the $\text{5th}$ toss (or the 6th level) we have four satisfying case.
5. etc.
i.e. in the $\text{kth}$ toss we would have $(k-1)$ satisfying case.
So,
$$\begin{align} E(x) &= \sum_{k=2}^{\infty } k.P(k)\\\ &= \sum_{k=2}^{\infty } k.\left \{ (k-1)*(0.5)^k \right \}\\ &= \sum_{k=2}^{\infty } \left \{ (k^2-k)*(0.5)^k \right \}\\ \end{align}$$
Using geometric series identity : https://en.wikipedia.org/wiki/Geometric_series#Geometric_power_series
$$\begin{align} \sum_{k=2}^{\infty}k(k-1)x^{k-2} = \frac{2}{(1-x)^3}\ \ \text{for } |x| < 1 \\ \end{align}$$
In our case : $x = 0.5$ So,
$$\begin{align} E &= \sum_{k=2}^{\infty}k(k-1)x^{k} = x^2\sum_{k=2}^{\infty}k(k-1)x^{k-2} = x^2.\frac{2}{(1-x)^3} \\ \end{align}$$
putting $x = \frac{1}{2}$ ; we get $E = 4$
More example:
For consecutive two heads ; HH
By drawing the tree diagram we can find the following series :

$$\begin{align*} E &= \sum{k.P(k) } \\ &=2.(1.x^2) + 3.(1.x^3) + 4.(2.x^4) + 5.(3.x^5)+6.(5.x^6)+7.(8.x^7)+.....\infty\\ \end{align*}$$
Above series is a nice combination of AP , generating function and Fibonacci numbers !!!!
- AP terms can be handled by integration or differentiation
- Fibanacci Generating function is = $\begin{align*} \frac{1}{1-x-x^2} \end{align*}$
$$\begin{align} &\Rightarrow \frac{E}{x} =2.(1.x^1) + 3.(1.x^2) + 4.(2.x^3) + 5.(3.x^4)+6.(5.x^5)+7.(8.x^6)+.....\infty\\ &\Rightarrow \int \frac{E}{x} .dx = 1.x^2+1.x^3+2.x^4+3.x^5+5.x^6+.....\infty \\ &\Rightarrow \int \frac{E}{x} .dx = x^2.\left ( 1.x^0+1.x^1+2.x^2+3.x^3+5.x^4+.....\infty \right ) \\ &\Rightarrow \int \frac{E}{x} .dx = \frac{x^2}{1-x-x^2} \\ &\Rightarrow \frac{E}{x} = \frac{\mathrm{d}}{\mathrm{d} x}\left [ \frac{x^2}{1-x-x^2} \right ] \\ &\Rightarrow \frac{E}{x} = \frac{2x(1-x-x^2)+(1+2x)x^2}{(1-x-x^2)^2} \\ &\Rightarrow E = x.\left \{ \frac{2x(1-x-x^2)+(1+2x)x^2}{(1-x-x^2)^2} \right \} \\ &\Rightarrow E = \frac{1}{2}.\left \{ \frac{2.\frac{1}{2}(1-\frac{1}{2}-\frac{1}{4})+(1+2.\frac{1}{2}).\frac{1}{4}}{(1-\frac{1}{2}-\frac{1}{4})^2} \right \} \\ &\Rightarrow E = 6 \\ \end{align}$$
Infact 2nd QS on HT can also be done in the above way using integration.
Correct Answer: $A$