Number of paths from $(0, 0)$ to $(n,n)$ that does not go above $x=y$ line is also known as Dyck path.
The number of Dyck path from $(0, 0)$ to $(n, n)$ is Catalan number
$C_n$ = ${2n} \choose{n}$$* \frac{1}{n+1}$
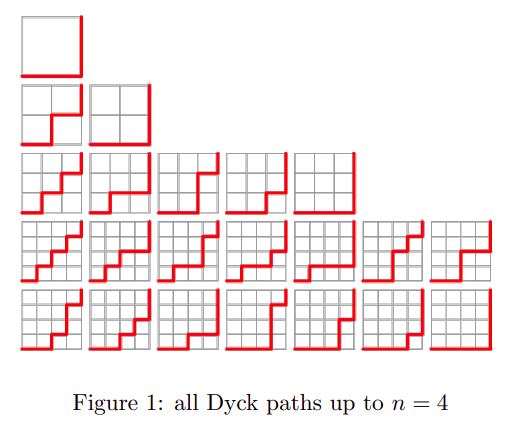
Source : https://www.math.toronto.edu/balazse/2019_Summer_MAT344/Lec_4.pdf
So for the above problem total number of path from $(0, 0)$ to $(n, n)$ is number of path that are below $x = y$ line + number of path that is above $x = y$ line
= $2 * C_3 = 2*5 = 10$