Consider a $3 \times 11$ rectangular grid as depicted in Figure $1,$ formed by $33$ tiles of area $1\text{m}^2.$ A staircase walk is a path in the grid which moves only right or up.
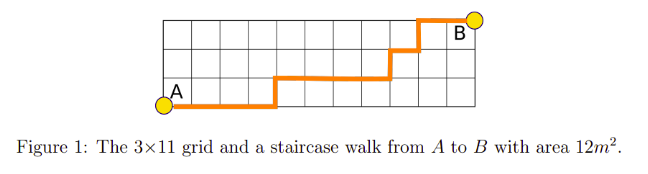
How many staircase walks are there from $\text{A}$ to $\text{B}$ which start by going to the right two times?