It is given in the question we have input as $n$ single digit base $10$ integers .
It has two cases ,
case 1:-
if $n \leq10$ then we have n distinct digit which can be sort trivially in constant amount of time .
So for case 1 it will take O(1) amount time .
Case 2:-
If $n >10$ then , it means we have repeated digits which can take values from $[0,9]$ .
So this can be done easily by traversing the array once and counting how many times each integers occurs from the given n integers.
The program looks like:-
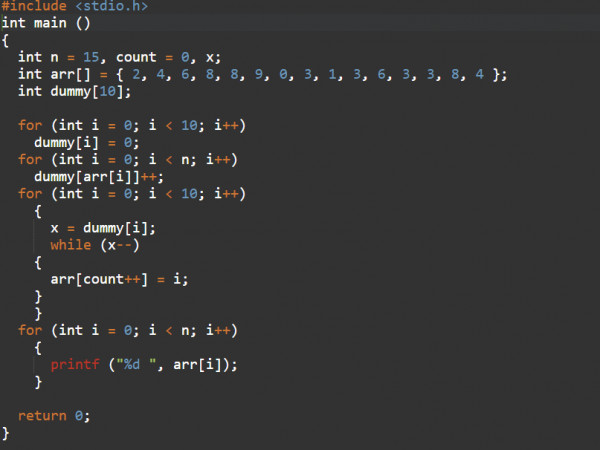
The complexity of the program is $\theta(n)$ .
So correct answer is (C) .