According the definition given to sink
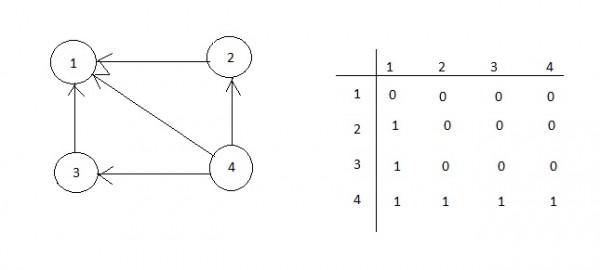
Now according to the definition we are checking the program. So, there must be incoming edge for the vertex of sink but those are not diagonal or not outgoing edges.
Now for i=0,j=1 , we check the condition if A[j][i] exists i.e !A[i][j] exists then take that vertex
like that i=0,j=2
i=0,j=3
Now, if() condition satisfies we make i=1 and j=2 (so here we are ignoring i=1 and j=1, means diagonal part)
Same thing happens while i=1,j=2
i=1,j=3
and if() condition checking.(as scope of j is local inside while loop , so post increment not change j value of outside while loop) makes i=2
...............
like that we can say E1: !A[i][j] and E2 : i = j;
------------------------------------------------------------------------------------------------------------------------------------
Now, flag initially 1 , we got a upper triangular matrix from the above code.
But according to the definition we have to get a lower triangular matrix
So, to change upper triangular matrix to lower triangular matrix
E3 will be B)(A[i][j] && !A[j][i]) where flag=0