Virtual Gate Test Series: Linear Algebra - Matrix(Number Of Solutions)

Question

$1)$ If the row reduced the form of a matrix has more than two non-zero entries in any row, then the corresponding system of equations has Infinitely many solutions.

$2)$ If the row reduced the form of a matrix has more than two non-zero entries in any row. then the corresponding system of equations either has infinitely many solutions or no solutions.

For infinite or no solutions, shouldn't the number of equations be less than the number of variables? If we have more than 2 non zero, then it's good, because then we will have more number of equations? How is the answer C?

Answer 1

Reduced row echelon form is used to find the nature of the solution set of the system.whether the solution is finite or infinite or single

A linear system is said to be consistent, if it has either one solution or infinitely many solutions. A system is inconsistent if it has no solutions.now first thing is how do we determine whether the system of linear equation is consistent or inconsistent , well consider a system of equations where we have 'n' columns or variables and 'm' numbers of rows or equations .In augmented matrix form if the right most column or the n+1 column is not a pivot or leading 1 ,we have a consistent system,otherwise we have an inconsistent system ,statement below is a theorem

THEOREM:

A).A linear system is consistent if, and only if the rightmost column of the augmented matrix is not a
pivot column.

Once it is decided that the our system is consistent we have a to find the number of dependent and independent or free variables.Again all the variables corresponding to the pivot columns are dependent variables and rest are free variables the system of equations below and its reduced echelon form shows the dependent and independent variables.

$[x_1a_1 + x_2a_2 + . . . + x_na_n = b]$ and its augmented matrix is  $[a_1 ,a_2 . . . a_n, b ]$

$\begin{bmatrix} 1 & -1 & 0 & 0 & 3 & 6 \\ 0 & 0 & 1 & 0 & -2 & 1 \\ 0 & 0 & 0 & 1 & 4 & 9 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}$

Here column $1,3 , 4$ are pivots while columns $2,5,6$ are not pivots or represent free variables.Here column 6 is not a pivot which shows that system of equation is consistent

equipped with information about the system consistency and free variables .we are able to find the nature of solution. Again a theorem

THEOREM:

B). If a linear system is consistent, and if there are no free variables, there exists only 1 solution. If
there are free variables, the solution set contains infinitely many solutions.
     

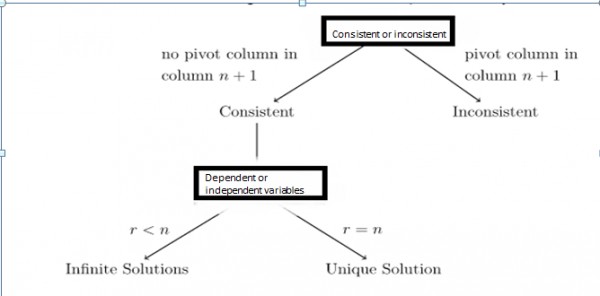
In picture above r is the number of pivots or non zero rows and n is the number variables

According to the above theorems and explanations C can only be true iff instead of no solution it is one solution.This question has some discrepancies.

A very good resource i found on this topic is available at http://linear.ups.edu/html/section-TSS.html