Here R represents real number space and $4$ represents the dimensionality (number of coordinates to represent a point in space) of the real number space . Consider the following 2 diagrams 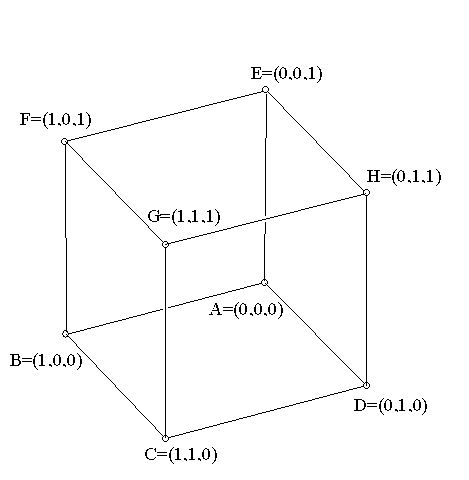

Dimensions
Each vertex of a cube is represented by $3$ coordinates $x,y,z$ . Since there are $3$ coordinates to represent each point on a cube so the cube is in three dimensional space. In case of this question there will be $4$ coordinates to represent a point
Orthogonal Matrices:
Orthogonal matrices have two special properties
- Each column has norm one, and each row has norm one.
-
Each column is orthogonal to every other column, and each row is orthogonal to every other row
Since there are no numerical values for a matrix given so your answer is simply C