So I have 1023 elements from 1-1023
What is the maximum depth at which element 9 can be placed?
For the purpose of working, I am considering as of now level(Root is at level 1), when we'll conclude we'll accordingly discuss about the depth.
So, suppose below is the min-heap structure(Remember here in question I have heap as a complete binary tree) under consideration I have taken for simplicity
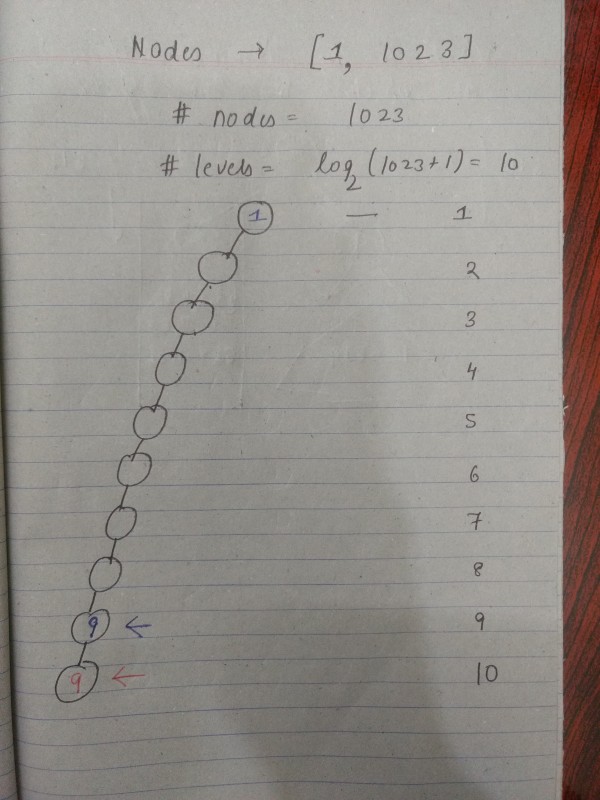
So, as we can see, 1 will be at the root.
In this tree of 1023 node we'll have 10 levels.
Suppose I place 9 on $10^{th}$ level. Now, between 1 and this 9 on level 10, I have to fill 8 values which are larger than 1 but smaller than 9, otherwise, 9 will end up propagating up the min -heap decreasing the level at which 9 is!!
But values which are greater than 1 and less than 9 are : 2,3,4,5,6,7,8=Only 7. That means between the chain shown above in diagram, If I place 9 on level 10, then I need to fill 8 elements which are greater than 1 but less than 9, but there are only 7 of them.
So, 9 cannot come at level 10.
Now, say I place 9 at level 9, so between 1 and 9 I need to place 7 values which are greater than 1 and less than 9, and Yes I can do so with help of 2,3,4,5,6,7,8.
So, maximum level at which 9 can appear is 9!!.
Since depth is the number of edges from root to node, we see that maximum depth of 9 is 8.
Since this heap is a complete binary tree as given in the question, I won't fall short of values when I'll place 9 on level 9, because elsewhere (all the part of min-heap which is not shown above) can be filled by remaining values.
Now Another question:
What is the minimum depth at which 9 can come?
Consider below image
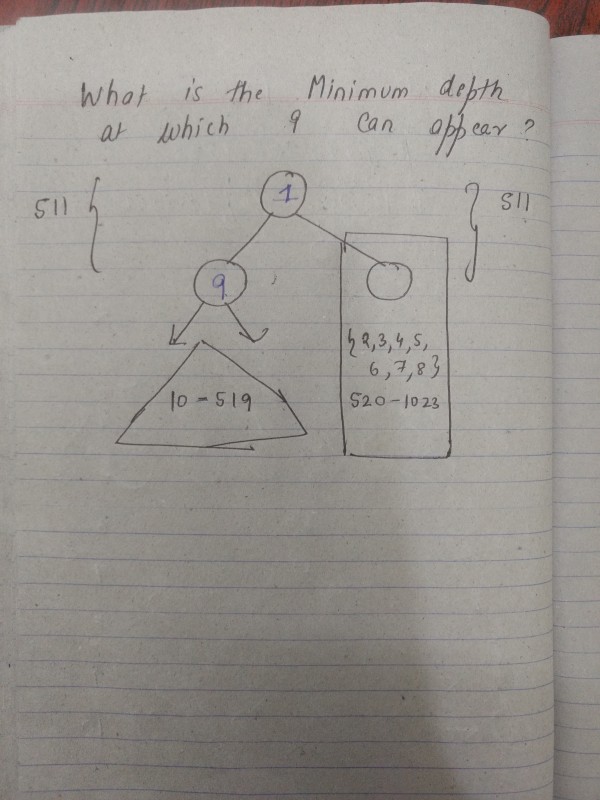
So root of this min-heap will be 1.
Suppose I place 9 on level 2.
Now, subtrees rooted at 1, both will contain $\frac{1023-1}{2}=511$ nodes each.
Now, subtree rooted at 9 will be min-heap and it will contain all $510$ nodes in total which are greater than 9.
Suppose I assign nodes 10-519 to sub-tree(Min-heap) rooted at 9.
Now, I have nodes remaining 2,3,4,5,6,7,8 and from 520-1023---> total 511 in the count. With these nodes, I can fill the right subtree of 1(which will also be a min-heap).
So, minimum level at which 9 can come here=2.
Hence Minimum Depth=1.