GATE CSE 2016 Set 2 | Question: 36

Question

Consider the following New-order strategy for traversing a binary tree:

• Visit the root;
• Visit the right subtree using New-order;
• Visit the left subtree using New-order;

The New-order traversal of the expression tree corresponding to the reverse polish expression

3 4 * 5 - 2 ^ 6 7 * 1 + - 

is given by:

• A. $+ -  1 \ 6 \ 7 * 2 \wedge 5 \ - \ 3 \ 4 \ *$
• B. $- +  1 *  6 \ 7 \wedge 2 - 5 * 3 \ 4$ 
• C. $- +  1 * 7 \ 6  \wedge 2 \ - \ 5 \ * \ 4 \ 3 $
• D. $1 \ 7 \ 6 *  + \ 2 \ 5  \ 4 \ 3 \ * \ - \wedge -$ 

Answer 1

Expression given in reverse polish notation (i,e in Post-order)

convert first it into In-order

$3\;4\;*\;5\;-\;2\;\wedge\;6\;7\;*\;1\;+\;-$

$(3*4)\;5\;-\;2\;\wedge\;6\;7\;*\;1\;+\;-$

$((3*4)-5)\;2\;\wedge\;6\;7\;*\;1\;+\;-$

$(((3*4)-5)\wedge 2)\;6\;7\;*\;1\;+\;-$

$(((3*4)-5)\wedge 2)\;(6*7)\;1\;+\;-$

$(((3*4)-5)\wedge 2)\;((6*7)+1)\;-$

$((((3*4)-5)\wedge 2)-((6*7)+1))$

so Inorder expression in $((((3*4)-5) \wedge 2)-((6*7)+1))$

New-Order traversal is as by ROOT RIGHT LEFT

$((((3*4)-5) \wedge 2)-((6*7)+1))$

$-((6*7)+1)(((3*4)-5) \wedge 2)$

$-+1(6*7)(((3*4)-5) \wedge 2)$

$-+1*7\;6(((3*4)-5) \wedge 2)$

$-+1*7\;6\wedge 2((3*4)-5)$

$-+1*7\;6\wedge 2-5(3*4)$

$-+1*7\;6\wedge 2-5*4\;3$

option C is correct

Answer 2

It is quite simple actually.

Postorder: left, right, root

Neworder: Root, right, left

(left, right, root) and (Root, right, left) are reverse of each other, right ?

So, these two traversals will be exact reverse of each other! Option (c)!

Comments

By looking at polish notation you can say that the order is post order

---

All operators are standard operators so their precedence and associativity is known. Moreover while doing conversion from postfix to infix, we are using operand stack and NOT operator stack! so associativity and precedence doesn’t affect the computation

---

If it strikes in your mind during the exam, you are going to kill the paper!

Answer 3

Another way to go => Answer C

1. Convert Postfix to Infix

2. Create expression tree.

3. Run the code !

Answer 4

$1)$  ${\fbox{3}}$ $\fbox{tos: 4}$

$2)$  ${\fbox{tos: 3*4}}$

$3)$  ${\fbox{3*4}}$ ${\fbox{tos: 5}}$

$4)$  ${\fbox{tos: ((3*4)-5)}}$

$5)$  ${\fbox{((3*4)-5)}}$ ${\fbox{tos: 2}}$

$6)$  ${\fbox{tos: (((3*4)-5)$\uparrow$ 2)}}$

$7)$  ${\fbox{(((3*4)-5)$\uparrow$ 2)}}$ ${\fbox{6}}$ ${\fbox{tos: 7}}$

$8)$  ${\fbox{(((3*4)-5)$\uparrow$ 2)}}$ ${\fbox{tos: 6*7}}$

$9)$  ${\fbox{(((3*4)-5)$\uparrow$ 2)}}$ ${\fbox{6*7}}$ ${\fbox{tos: 1}}$

$10)$  ${\fbox{(((3*4)-5)$\uparrow$ 2)}}$ ${\fbox{tos: ((6*7)+1)}}$

$11)$  ${\fbox{((((3*4)-5)$\uparrow$ 2)-((6*7)+1))}}$

$infix: ((((3*4)-5)\uparrow 2)-((6*7)+1))$

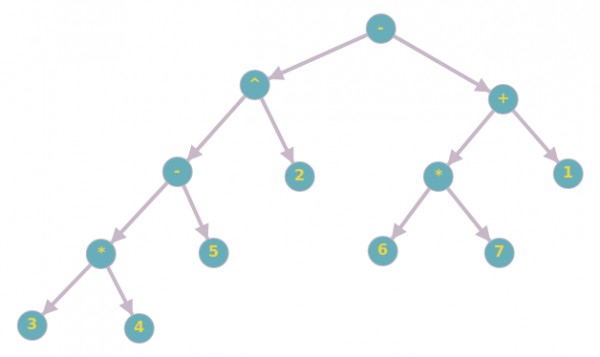
$New-order:Root-right-left$

$-+1*76\uparrow 2-5*43$

---

$Ans: C$