GATE CSE 2016 Set 1 | Question: 14

Question

Let $G$ be a weighted connected undirected graph with distinct positive edge weights. If every edge weight is increased by the same value, then which of the following statements is/are TRUE?

• $P$: Minimum spanning tree of $G$ does not change.
• $Q$: Shortest path between any pair of vertices does not change.

• A. $P$ only
• B. $Q$ only
• C. Neither $P$ nor $Q$
• D. Both $P$ and $Q$

Comments

Can have a look at this question also for $Q.$

https://gateoverflow.in/47090/cmi2012-b-05b

---

try out this pyq to see if you truly understood the concept or not

https://gateoverflow.in/8499/gate-cse-2015-set-3-question-40#a_list

---

Good Explanation By rajesh pradhan 

https://gateoverflow.in/39673/gate-cse-2016-set-1-question-14?show=69679#a69679

Answer 1

Q is false because if all the edge weights are increasing by the same value then there is a  possibility that the shortest path between the 2 vertices may change for eg: 

---

Suppose we have to find a shortest path between vertices A and E. Vertex A is connected to B and D. B is connected to C. C and D are connected to E. 

The weight of the edges are:

AB=4

BC=4

CE=4

AD=6

DE=7

so we can reach from A to E via Band C or via D

path1:A ->B->C->E=4+4+4=12

path2:A->D->E=6+7=13

So the shortest path is path1.

Now if thw weight of each edge is increased by 3

the new weight of path1 is:7+7+7=21

and path2 is:9+10=19

So now the shortest path is path2. 

Hence proved by contradiction that Q is False.

Comments

Here they clearly mentioned that edge weights should be distinct..

Answer 2

“If every edge weight is increased by the same value” it simply means take any

constant C and add it to every edge that is there in the graph.

 

Why the MST will not change ?

PROOF:

MST simply means connecting n vertices using n-1 edges, keeping the sum of edge

weights as low as possible. So basically it reduces to a equation.

w1 +  w2 + w3 + . . . . . .  =  m   (previous MST)

W1 +  W2 + W3 + . . . . .   =  M   (New MST after adding constant weight)

 

we need to show that all the new edges maps exactly with old edges.

Considering kruskal’s algorithm, first we select the edge with least weight,

check for cycle and if everything seems good we add it to our MST and repeat,

increasing the weights on every edge will have no change in the

working of the algorithm, as the comparison based selection criteria

remains unaffected, same goes for Prim’s algo. also,

hence we are bound to get the same MST.

 

The Q part is wrong as we can easily think of a counter case for this.

We are using 2 as our constant weight.

 

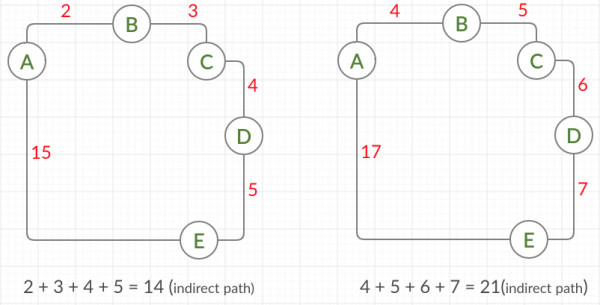
The shortest path between A and E has been changed.

 

Answer 3

P is true.

Theres an ambiguity in the question regarding Q, but still answer is same, take any context.

If every edge weight is increased by the same value

This could mean :

1. We are increasing the value of each edge overall and form a different graph itself, in that case it doesn’t really matter, the multiple paths before will stay multiple paths as usual.
2. We are increasing the edge as we go in same graph itself, if A-B is x, we set B-C as x+2 ; C-D = x+2+2 ; In any case we can still have multiple paths possible like : 

So be it any context, Q is false.

Answer 4

for Stateemt  P

for Statemetn  Q