Draw the graph by considering the values given in the matrix as:


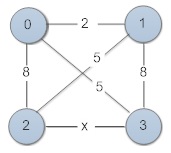
We have to find the largest possible integer value of x for which at least one shortest path between some pair of vertices will contain the edge (3,2) that is x.
After we draw the graph we can find it in couple of seconds like this-
For Smallest possible integer value of x:
From vertex 3: The weight of the edge (3,1) is 8. We can reach vertex 1 via vertex 2 in less than 8 cost i.e if value of x is 0,1 or 2 than cost can be 5 (i.e 0+5), 6(i.e 1+5) or 7(i.e 2+5) respectively.
For Largest possible integer value of x:
From vertex 3 We can reach vertex 2 via vertex 0 in 13 cost. But we can reach vertex 2 via edge (3,2) if value of x is 12 (i.e largest possible).
Hence, Largest possible value of x =12.