First, we'll see what $f1(8)$ will return
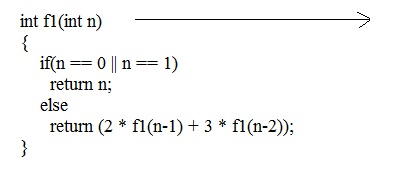
int f1(int n)
{
if(n == 0 || n == 1)
return n;
else
return(2*f1(n-1) + 3 * f1(n-2));
}
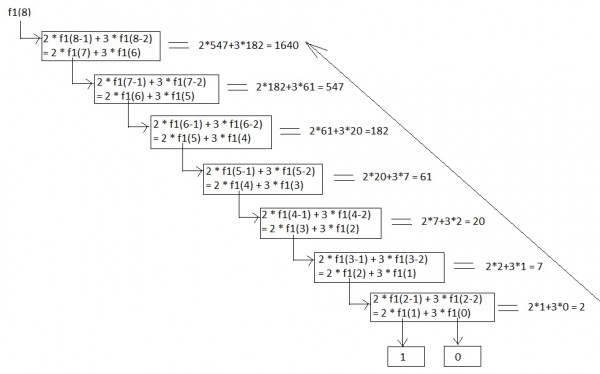

∴ $f1(8)$ returns $1640$
Now, what $f2(8) $ will return --
int i;
We can take any values of $i$, but at the end, we want the return value as $X[n]$, so we'll going to take $i=8$
int X[N], Y[N], Z[N];
The above line creates $3$ arrays
X[0] = Y[0] = Z[0] = 0;
This will set all the index $0$ position of all the $3$ arrays to $0$
X[1] = 1; Y[1] = 2; Z[1] = 3;
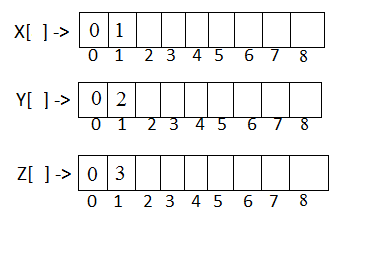
for(i=2; i<= n; i++)
This loop will run from $i=2$ to $i=8$
X[i] = Y[i-1] + Z[i-2];
Y[i] = 2 * X[i];
Z[i] = 3 * X[i];
when $i = 2$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[2] = Y[2-1] + Z[2-2] \\ = Y[1] + Z[0] = 2 + 0 \\ = 2$
$Y[i] = 2 * X[i]$ $\rightarrow Y[2] = 2 * X[2] \\ = 2 * 2 \\ = 4$
$Z[i] = 3 * X[i]$ $\rightarrow Z[2] = 3 * X[2] \\ = 3 * 2 \\ = 6$

when $i = 3$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[3] = Y[3-1] + Z[3-2] \\ = Y[2] + Z[1] = 4 + 3 \\ = 7$
$Y[i] = 2 * X[i]$ $\rightarrow Y[3] = 2 * X[3] \\ = 2 * 7 \\ = 14$
$Z[i] = 3 * X[i]$ $\rightarrow Z[3] = 3 * X[3] \\ = 3 * 7 \\ = 21$

when $i = 4$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[4] = Y[4-1] + Z[4-2] \\ = Y[3] + Z[2] = 14 + 6 \\ = 20$
$Y[i] = 2 * X[i]$ $\rightarrow Y[4] = 2 * X[4] \\ = 2 * 20 \\ = 40$
$Z[i] = 3 * X[i]$ $\rightarrow Z[4] = 3 * X[4] \\ = 3 * 20 \\ = 60$

when $i = 5$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[5] = Y[5-1] + Z[5-2] \\ = Y[4] + Z[3] = 40 + 21 \\ = 61$
$Y[i] = 2 * X[i]$ $\rightarrow Y[5] = 2 * X[5] \\ = 2 * 61 \\ = 122$
$Z[i] = 3 * X[i]$ $\rightarrow Z[5] = 3 * X[5] \\ = 3 * 61 \\ = 183$
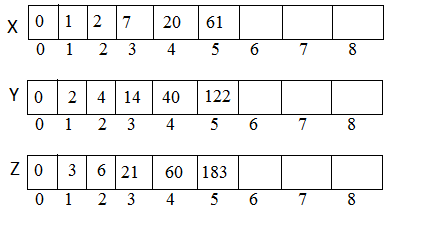
when $i = 6$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[6] = Y[6-1] + Z[6-2] \\ = Y[5] + Z[4] = 122 + 60 \\ =182$
$Y[i] = 2 * X[i]$ $\rightarrow Y[6] = 2 * X[6] \\ = 2 * 182 \\ = 364$
$Z[i] = 3 * X[i]$ $\rightarrow Z[6] = 3 * X[6] \\ = 3 * 182 \\ = 546$
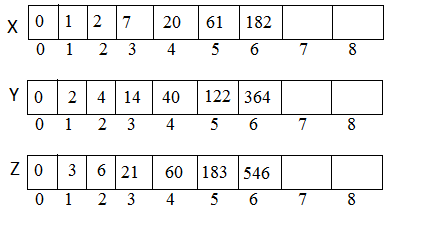
when $i = 7$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[7] = Y[7-1] + Z[7-2] \\ = Y[6] + Z[5] = 364 + 183 \\ = 547$
$Y[i] = 2 * X[i]$ $\rightarrow Y[7] = 2 * X[7] \\ = 2 * 547 \\ = 1094$
$Z[i] = 3 * X[i]$ $\rightarrow Z[7] = 3 * X[7] \\ = 3 * 547 \\ = 1641$
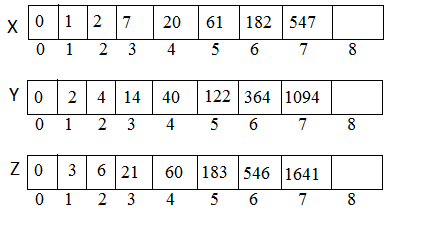
when $i = 8$ ,
$X[ i ] = Y[ i-1 ] + Z[ i-2 ]$ $\rightarrow X[8] = Y[8-1] + Z[8-2] \\ = Y[7] + Z[6] = 1094 + 546 \\ = 1640$
$Y[i] = 2 * X[i]$ $\rightarrow Y[8] = 2 * X[8] \\ = 2 * 1640 \\ = 3280$
$Z[i] = 3 * X[i]$ $\rightarrow Z[8] = 3 * X[8] \\ = 3 * 1640 \\ = 4920$
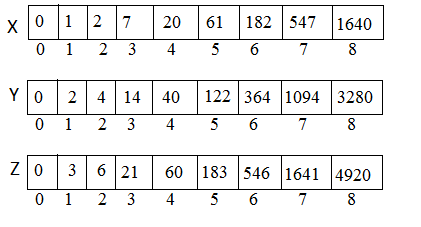
Now we'll be coming out from for loop & execute the last statement
return X[n];
which will return $X[n]$ i.e. $X[8]$ which is $1640$
∴ $f1(8)$ will return $1640$ & $f2(8)$ will also return $1640$
The correct option will be C).