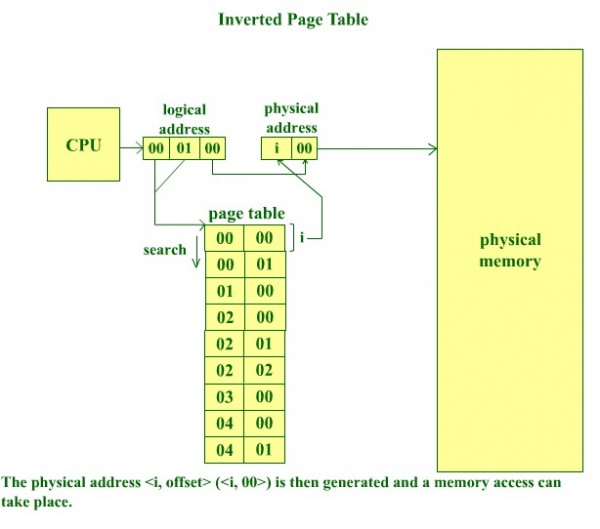
Inverted page table is a global page table maintained by the operating system for all the processes. There is just one page table in the entire system, implying that additional information needs to be stored in the page table to identify page table entries corresponding to each process.
here no of pages are possible = 231 / 213 =218
for ex