Answer:
Check following NFA. I've done subset construction too. $8$ States are needed even after minimization.
Every state containing D is final state.
NFA:
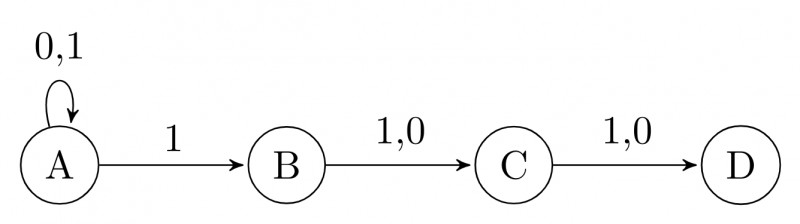
NFA to DFA
$$\begin{array}{|l|l|l|}\hline \text{} & \text{0} & \text{1} \\\hline \text{A} & \text{A} & \text{AB} \\ \text{AB} & \text{AC} & \text{ABC} \\ \text{AC} & \text{AD} & \text{ABD}\\ \textbf{AD} & \text{A} & \text{AB} \\ \text{ABC} & \text{ACD} & \text{ABCD} \\ \textbf{ABD} & \text{AC} & \text{ABC} \\ \textbf{ACD} & \text{AD} & \text{ABD}\\ \textbf{ABCD} & \text{ACD} & \text{ABCD} \\\hline \end{array}$$
The third symbol from the right is a '$1$'. So, we can also consider the Myhill-Nerode theorem here. Intuitively we need to remember the last $3$ bits of the string each of which forms a different equivalence class as per the Myhill-Nerode theorem as shown by the following table. Here, for any set of strings (in a row), we distinguish only the rows above it - as the relation is symmetric. Further strings in the language and not in the language are distinguished separately as $\epsilon$ distinguishes them.
$$\begin{array}{|l|c|l|l|}\hline \text{} & \textbf{Last}\ \textbf{3}\ & \textbf{Distinguishing string} & \textbf{In L?}\\
&\textbf{bits}\\
\hline 1 & 000 & \text{} & \text{N} \\ \hline
2 & 001 & \text{$“00$" distinguishes from strings in $1$.} & \text{N} \\\hline
3 & 010 & \text{“$0$" distinguishes from strings in $1$ and $2$.} & \text{N} \\
&& \text{“$00$" distinguishes from strings in $4$.}\\\hline
4 & 011 & \text{“$0$" distinguishes from strings in $1$ and $2$.}& \text{N} \\
&&\text{“$00$" distinguishes from strings in $3$.}\\\hline
5 & 100 & \text{} & \text{Y} \\\hline
6 & 101 & \text{“$00$" distinguishes from strings in $5$.} & \text{Y} \\\hline
7 & 110 & \text{“$0$" distinguishes from strings in $5$.} & \text{Y}\\
&&\text{“$00$" distinguishes from strings in $6$.}\\\hline
8 & 111 & \text{“$00$" distinguishes from strings in $5$ and $7$.} & \text{Y}\\
&&\text{“$0$" distinguishes from strings in $6$.}\\\hline \end{array}$$