If we consider given In-order and Post Order and construct the tree then no option is going to match .
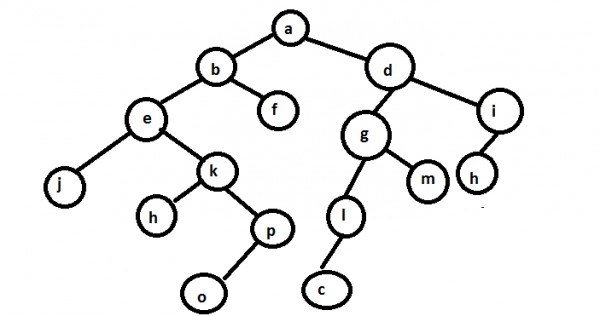
This is the tree with given in-order and post-order
If you traverse it from top to bottom left to right and print each element second time then we are going to get the exact in-order given in question .
if we print the element last time then we are going to get the post-order. But for pre-order it does not give us any option from given options, So correct pre-order should be
Preorder : abejknpofdglcmih