search success nodes (or keys) are
< do , if , int , while > in ascending order.
a(i) < x < a(i+1) is nothing but a comparison criteria of searching.
If we search something (= p) in between do and if. We would not be able to find p because we simply don't have such node (=p). We can consider that a search failure node, since p is not there in the binary search tree. Corresponding search probabilities of pi given in the question as q[ ] array. Since we have 4 nodes do,if,int,while we have five location of fail search (how five ? p1 do p2 if p3 int p4 while p5) So, five locations where possibility of search failure is there.
If we see all the nodes in ascending order they are :
p1,do,p2,if,p3,int,p4,while,p5 with probability of search 3/8, 3/8, 1/8, 1/8, 2/8, 3/8, 1/8, 1/8, 1/8.
Option C and D are invalid tree.
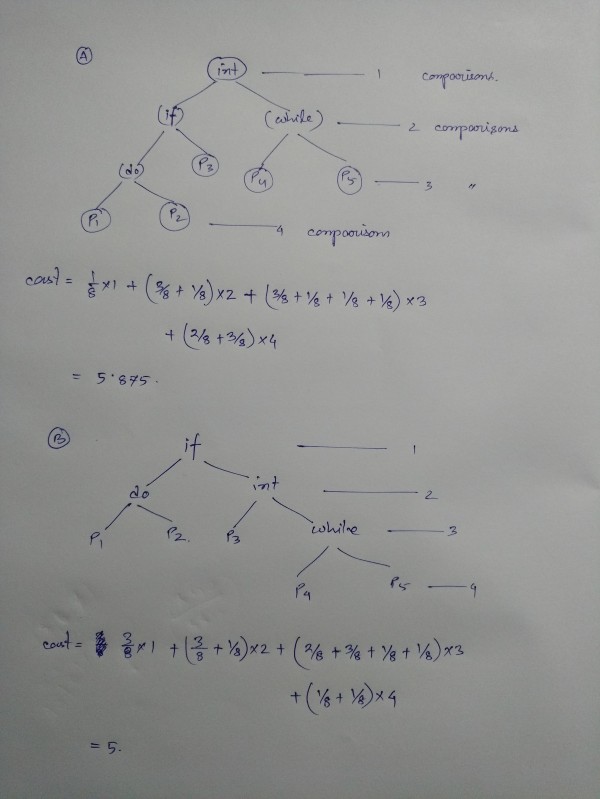
So answer is B