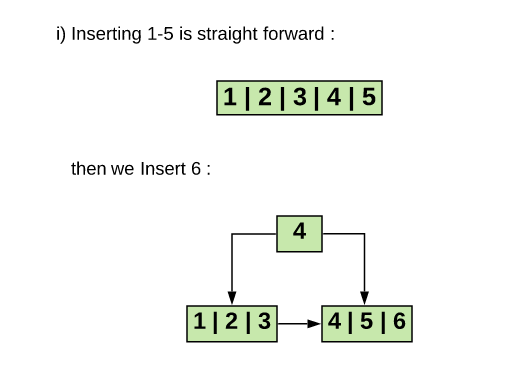
A.i)
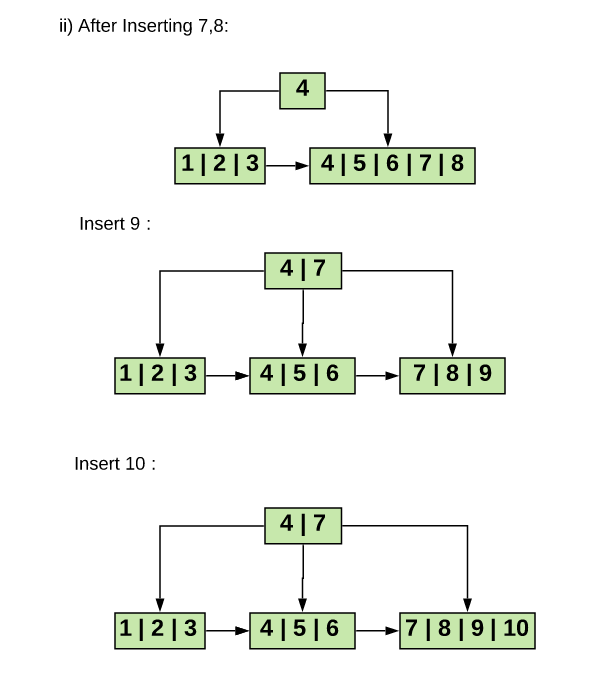
A.ii)
B)

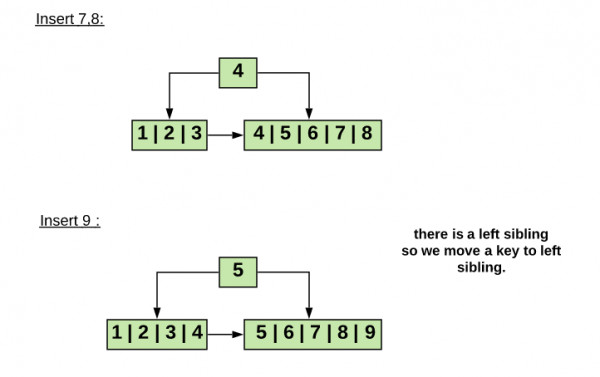
The next 2 insertions weren’t asked in the question but will help you to understand part C of this question.
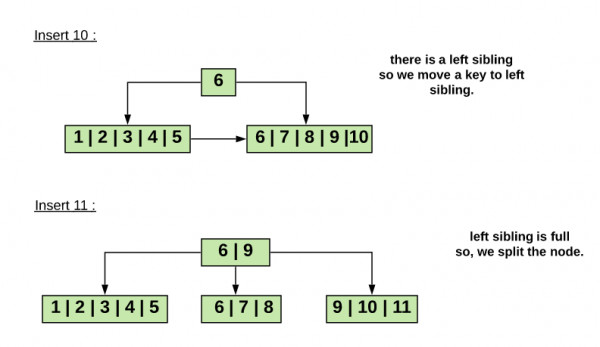
C. Insert a LONG SEQUENCE of keys in INCREASING ORDER
- In normal case: Insertion always will be done at the rightmost leaf node, and all nodes will have exact $\lfloor \frac{m+1}{2} \rfloor $ keys expect this rightmost leaf ( no of keys can vary from $\lfloor \frac{m+1}{2} \rfloor $ to $m$ for rightmost leaf).
For a long sequence, we can say the average is approximately $\lfloor \frac{m+1}{2} \rfloor $ (This is the answer).
(There are two possible answers for this part, I left it on the reader to find out the second one)
Because all nodes will have $\lfloor \frac{m+1}{2} \rfloor $ keys except $1$ rightmost node.
we can also find the exact average in this case:
Let there are $n$ keys in total ( inserted in increasing order),
No of leaf nodes will be exactly $\left \lfloor \frac{n}{\left \lfloor \frac{m+1}{2} \right \rfloor} \right \rfloor$
Average number of keys in leaf would be: $\frac{n}{\left \lfloor \frac{n}{\left \lfloor \frac{m+1}{2} \right \rfloor} \right \rfloor}$
- With insertion as in (B): In this case, we can observe until the left sibling is full, we are shifting a key to the left leaf. As we insert more and more keys all leaf nodes are filled except the rightmost two leaves, the rightmost $2$ leaves can have any number of in $\lfloor \frac{m+1}{2} \rfloor $ to m each.
For a long sequence, we can say the average is approximately $m$. ( Same reasoning as case i )
we can find the actual average in this case as well,
Let there are $n$ keys in total ( inserted in increasing order),
Number of leaf nodes in this case will be $\left \lceil \frac{n}{m} \right \rceil$,
so average number of keys would be: $\frac{n}{\left \lceil \frac{n}{m} \right \rceil}$