Expectated no of coin toss

Question

An unbiased coin is tossed repeatedly and outcomes are recorded. What is the expected no of toss to get HT ( one head and one tail consecutively) ?

Answer 1

Let  E is the expected no of turn to get first HT.

And E' = expected no of turns when 1st one is head.

Now when 1st one is T, then we just lost our first chance, because to get HT first we need to get H first.

So,  E = 1/2 ( E + 1) + 1/2 ( E' +1 )   ------------------(A)

When we get H in first turn then if we get T in next turn then we reach our destination.

And if again H comes in the next turn then 1st H gets wasted.

So, E' = 1/2 ( 1)  + 1/2 ( E' + 1)

=>  E' = 2.

Now lets put  E' in equation (A),

      E = (E + 1) / 2 + (2 + 1) /2

=> 2E = E + 1 + 3

       E = 4 . (Ans)  

Comments

Thanks ! Few things are more clear now. I was also feeling the need of two random variables.

E = Expected toss to get a H ($E_H$) Or Expected no of toss to get a T ($E_T$) is indeed 2.

$\begin{align*} E &= 1.\frac{1}{2^1} + 2.\frac{1}{2^2} + 3.\frac{1}{2^3} + 4.\frac{1}{2^4} ... + \infty \\ &= 2 \end{align*}$

And If we first (in the beginning) get H, then following two are the same thing :

• Wasted one toss and and get a T  => 1+ $E_T$
• Got an H, find a T => $E_H$ + 1 (you used !)

Answer 2

Let E be the Expected no of tosses of coin.

we have 2 cases

T
H(till we not get T) i.e. HT,HHT,HHHT.....

1)Start tossing if we get Tail first (probability=1/2) then we are at the same point where we started except we have wasted 1 flip.

it is represented by 1/2(E+1)

2)Similarly,if we get Head in first toss we have (probability=1/2) but in next toss we are counting till we not get tail(T)

it is represented by 1/2[1/2+1/2(E+1)]
here first term outside bracket indicate probability of getting head first time and in inner bracket first term represent probability of getting tail and second term represent probability we get head and we are flipping again wasting 1 flip.
Putting all three case together we have

E=1/2(E+1)+ 1/2[1/2+1/2(E+1)]

4E=3E+4

 E=4

Comments

second case begins like HT,HHT,HHHT.....so probabilty first toss is head is 1/2 and probailty second or after that we get tail is 1/2(probabilty tail i.e HT) +1/2(E+1)(probabilty second toss head after that we get tail i.e HHT,HHHT...)....overall equation is 1/2[1/2+1/2(E+1)]

---

E represent no of toss in the main tree ( starting structure)  to get HT.

E+x means

current accumulated cost is x , but we arrive at the same tree structure ( subproblem) as in the starting, that's why adding E. Which gives the recursive nature.

Your second case is skewed, but still E+x format is appearing.

---

@dd Sir, in the context you mentioned " E = 1/2 ( E+1 ) + 1/2 [ 1/2 + 1/2 ( E+1 ) ] "

 but is it not "  E = 1/2 ( E+1 ) + 1/2 [ ( 1/2 * 2 ) + 1/2 ( E+1 ) ] " to explain that for HT gets  E length as ' 2 '.

if not why? and where I am wrong?

 

Answer 3

I tried to solve above question using the following probability tree diagram.

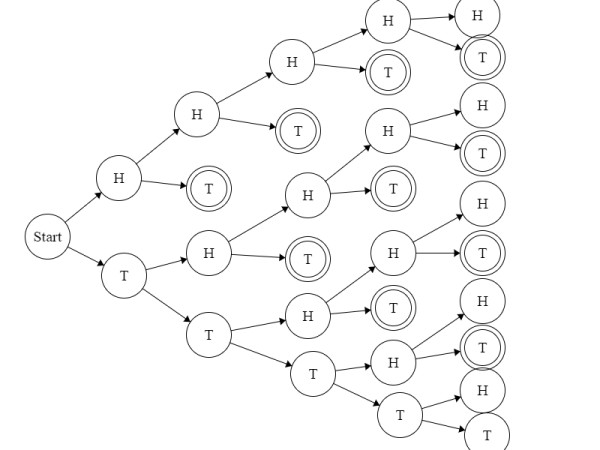
Probability in each branch is = $0.5$. I double circled the satisfying toss events.
While observing the diagram I noticed that, from 2nd toss onward our required event starts showing up. Additionally,

 1. in the $\text{2nd}$ toss (or the 3rd level) we have one satisfying case.
 2. in the $\text{3rd}$ toss (or the 4th level) we have two satisfying case.
 3. in the $\text{4th}$ toss (or the 5th level) we have three satisfying case.
 4. in the $\text{5th}$ toss (or the 6th level) we have four satisfying case.
 5. etc.

i.e. in the $\text{kth}$ toss we would have $(k-1)$ satisfying case.
So,

$$\begin{align*} E(x) &= \sum_{k=2}^{\infty } k.P(k)\\\ &= \sum_{k=2}^{\infty } k.\left \{ (k-1)*(0.5)^k \right \}\\ &= \sum_{k=2}^{\infty } \left \{ (k^2-k)*(0.5)^k \right \}\\ \end{align*}$$

Uisng geommetric series identity : https://en.wikipedia.org/wiki/Geometric_series#Geometric_power_series

$$\begin{align*} \sum_{k=2}^{\infty}k(k-1)x^{k-2} = \frac{2}{(1-x)^3}\ \ \text{for } |x| < 1 \\ \end{align*}$$

In our case : $x = 0.5$ So,

$$\begin{align*} E &= x^2\sum_{k=2}^{\infty}k(k-1)x^{k-2} = \frac{2x^2}{(1-x)^3} \\ \end{align*}$$

putting $x = \frac{1}{2}$   ; we get $E = 4$