It is a 5 by 7 grid with one trap state. Language is consists of 12 length strings and to get one such string, we can choose any 5 spot for a's and rest 7 spot will be for b's.
Like the following has exactly 2 a's and 2 b's
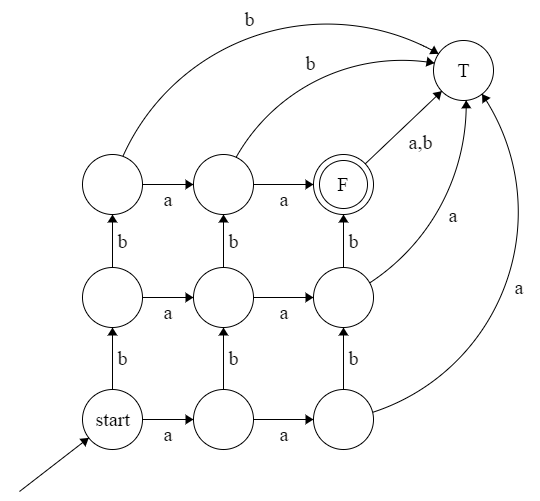
As we need ( 3 * 3 + 1 ) = 10 states for 2 a's and 2 b's.
Similarly, For 5 a's and 7 b's, we need ( 6 * 8 + 1) = 49 states.
This problem resembles to a good combinatorial problem of finding no of paths in such a graph from start node to end node.