A) An unambiguous grammar has same leftmost and rightmost derivation
This statement is false, let me take an example, suppose given unambiguous gammer is
S -> AB
A -> a
B -> b
Suppose our input string is ab
Left Most Derivation
S -> AB -> aB -> ab
Right Most Derivation
S -> AB -> Ab -> ab
Notice Left Most derivation and Right most derivation are not same, still gammer is unambiguous.
Here is the Derivation Tree
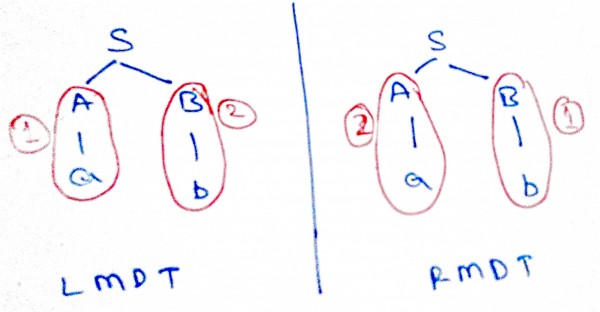
So for a given gammer, we can have same Left most derivation Tree and Right most derivation tree, but left most derivation and right most derivation may vary.
B) An LL(1) parser is a top-down parser : True
C) LALR is more powerful than SLR : True
D) An ambiguous grammar can never be LR(k) for any k : True
So only False option is (a).