I think all options are right here.
A)True-Because if a tree have more than n-1 edges it will form cycle.
B)True
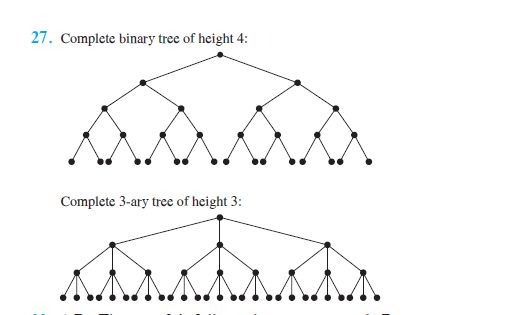
D)True)---In complete binary tree with height h, no. of nodes are 2h+1–1
C)True)-->According to "Discrete Mathematics and Its Applications" by " Kenneth H. Rosen"
page no-1018
Page.no-777
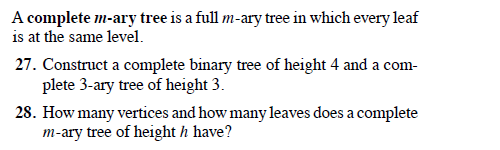
http://www2.fiit.stuba.sk/~kvasnicka/Mathematics%20for%20Informatics/Rosen_Discrete_Mathematics_and_Its_Applications_7th_Edition.pdf
And in a binary tree if there are n+1 leafs then there are n nodes with exactly 2 childs.
So in complete binary tree given above,if there are n internal nodes then all of them will have 2 childs,so total no of leafs are n+1.
Also there are slight variations in the defination of complete binary tree,so it should be provided in question.